This is the first part in a series of tutorials on stoichiometry. Stoichiometry is the area of chemistry that involves determining the masses (in grams) and amounts (in moles) of reactants and products of a chemical reaction using a balanced chemical equation.
This tutorial will involve determining the masses in grams of reactants and products of a chemical reaction. This can be done via two methods: one involving cancelling units not needed for an answer with conversion factors and one that doesn’t involve this additional step.
The following tutorial will contain stoichiometric calculations without the use of conversion factors to cancel out units. If you would like to see how stoichiometric calculations can be done with conversion factors to cancel out units, please refer to ‘Determining the Masses of Reactants and Products of a Chemical Reaction (with Conversion Factors)’.
I would advise you seek advice from your teacher, lecturer or tutor on whether you should use conversion factors for cancelling out units in stoichiometric calculations (as the requirements of different course specifications vary).
Balancing Equations and Mole Ratio
The first important thing to note about stoichiometry is that you must ensure a chemical equation which signifies a chemical reaction is balanced. This means the same number of atoms or ions of each particular element is present on the reactant side of the equation (the left side of the equation) and the product side of the equation (the right side of the equation).
The balancing of a chemical equation is done to ensure it corresponds with the law of conservation of mass.
This law states that mass is neither created nor destroyed during a chemical reaction, meaning the total mass of the reactants is equal to the total mass of the products. This means that atoms or ions are not created or destroyed during a chemical reaction – they just become part of a different chemical substance.
So, how do we balance an equation? Well we can’t change the number of atoms or ions present in each individual atom, molecule or formula unit of a substance – which means we can’t change the chemical formulas in the equation. However, we can change the number of moles of each chemical substance participating in a reaction. This is done by including stoichiometric coefficients in a chemical equation.
Stoichiometric coefficients are numbers which signify the number of moles of each reactant and product in a chemical reaction. They are placed before the chemical formula of each substance and this can alter the total number of atoms or ions of a particular element on a side of a chemical equation.
Let’s look at an example.
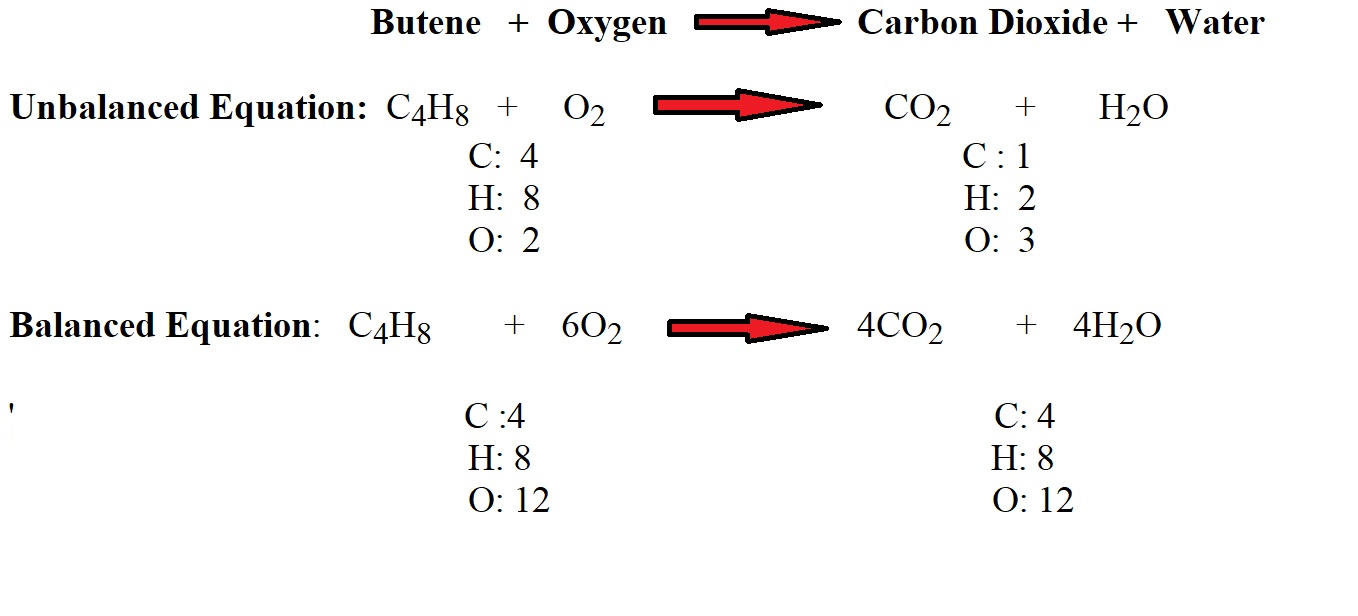
The equation above represents a reaction in which butene combusts when it reacts with oxygen (with some heat) to produce carbon dioxide and water. The unbalanced equation and the tally of the number of atoms present shows that there is an imbalance in the number of carbon, hydrogen and oxygen atoms present on the two sides of the equation. This means the reactants and the products will have different total masses and therefore will not adhere to the law of conservation of mass.
However, the inclusion of stoichiometric coefficients signifies a higher number of moles of oxygen as a reactant and higher numbers of moles of carbon dioxide and water as products. This then allows us to balance the equation (same number of atoms of each element on both sides of the equation) and ensure the total masses of reactants and products are equal, thereby adhering to the law of conservation of mass.
The inclusion of stoichiometric coefficients creates a mole ratio (also known as a stoichiometric ratio).
This describes the ratio of the number of moles of one substance to the number of moles of another substance. This means for every certain number of moles of one substance that acts as a reactant in a forward reaction you will get a certain number of moles of another substance as a product.
Alternatively, it can indicate that a certain number of moles of a product reacts to form a certain number of moles of a reactant following a reverse reaction, because some reactions are reversible.
The mole ratio illustrated in a balanced chemical equation is key to working out the amounts (in moles) and subsequently the masses of the reactants and products of a chemical reaction. Let’s see how that’s the case with some calculations.
Question 1
Sodium nitrate decomposes to sodium nitrite and oxygen when heated.
Calculate the mass of oxygen produced from 82.0 g of sodium nitrate (NaNO3).
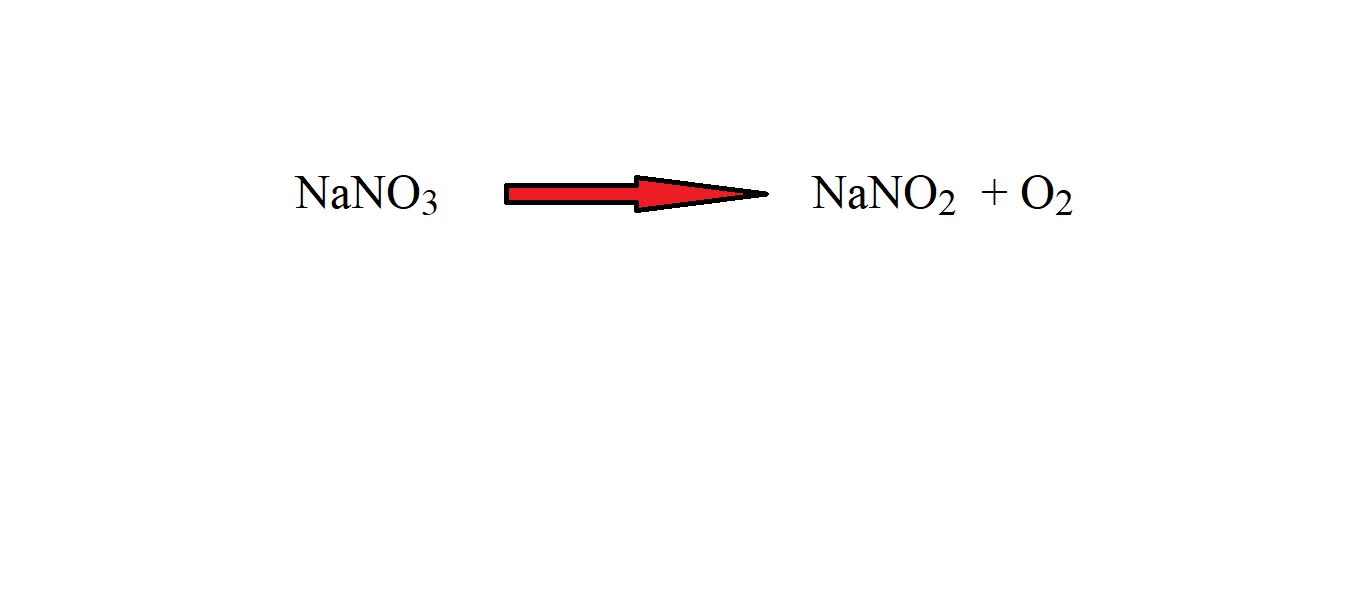
Step 1: Write out the reaction as an equation with the correct chemical formulas.
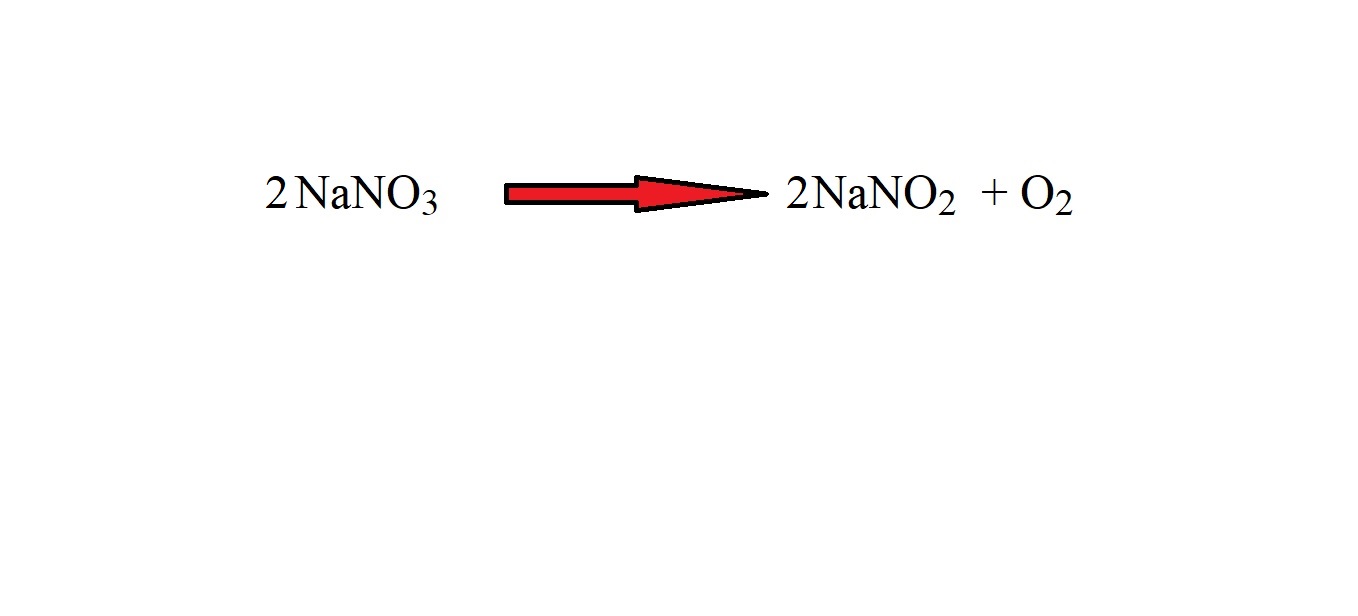
Step 2: Balance the equation using stoichiometric coefficients.
Step 3: Work out the molar mass of the substance you know the mass of. In this example that would be sodium nitrate.
Reminder: Molar mass is the mass of one mole of a substance. The molar mass does not change no matter what stoichiometric coefficient is in front of the formula.
M = 23.0 + 14.0 + (3 x 16.0) = 85.0 g mol-1
Step 4: Calculate the amount in moles of the substance you know the mass and molar mass of using the following formula:
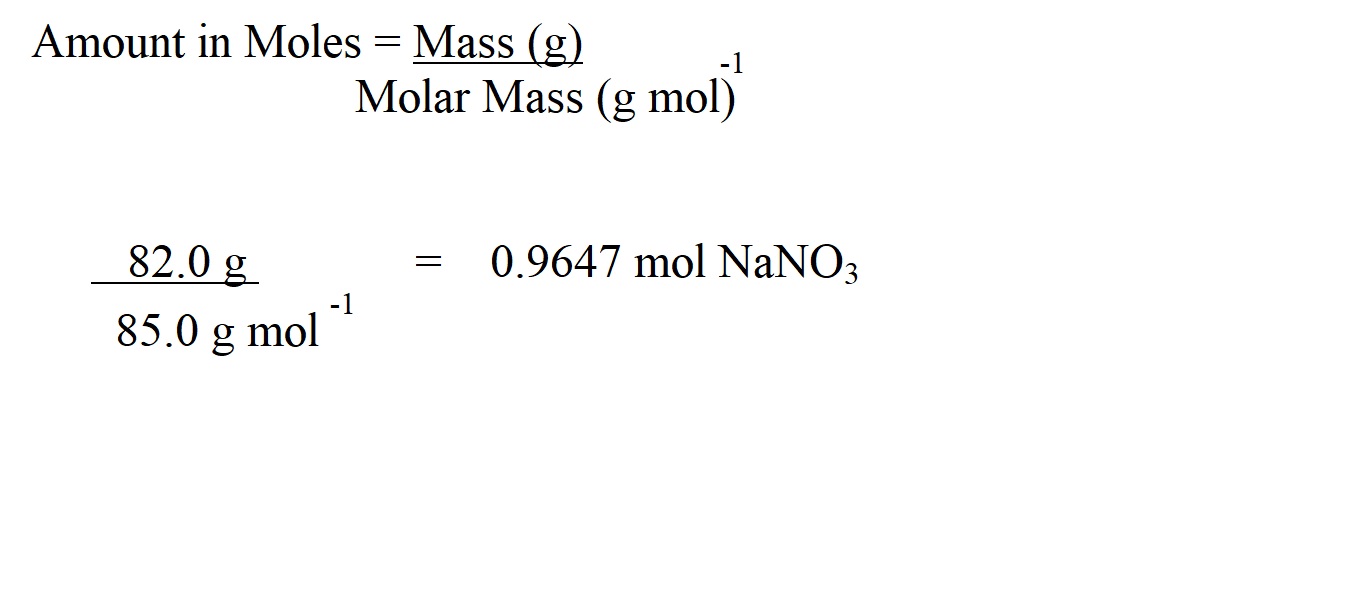
The amount in moles of sodium nitrate has been given to four significant figures because this isn’t the final answer to our question and we don’t want to round to too few significant figures early in the calculation because we want to avoid inaccuracy in our final answer.
We need to work out the amount in moles of the substance we know the mass of first in order to then work out the amount in moles and mass of the substance we don’t know the mass of.
Step 5: Use the mole ratio (stoichiometric ratio) indicated by the balanced equation to work out the amount in moles of the substance in the chemical reaction of which you want to work out the mass of. In this question that would be oxygen.
Let’s look at the balanced equation again for the reaction.

The absence of a stoichiometric coefficient in an equation before a chemical formula does not mean 0 – it means that there is 1 mole of that substance (we just don’t tend to write 1 as a stoichiometric coefficient).
The mole ratio of sodium nitrate to oxygen is 2 moles to 1 mole. This means that to work out the amount in moles of oxygen, we must divide the amount in moles of sodium nitrate by 2.
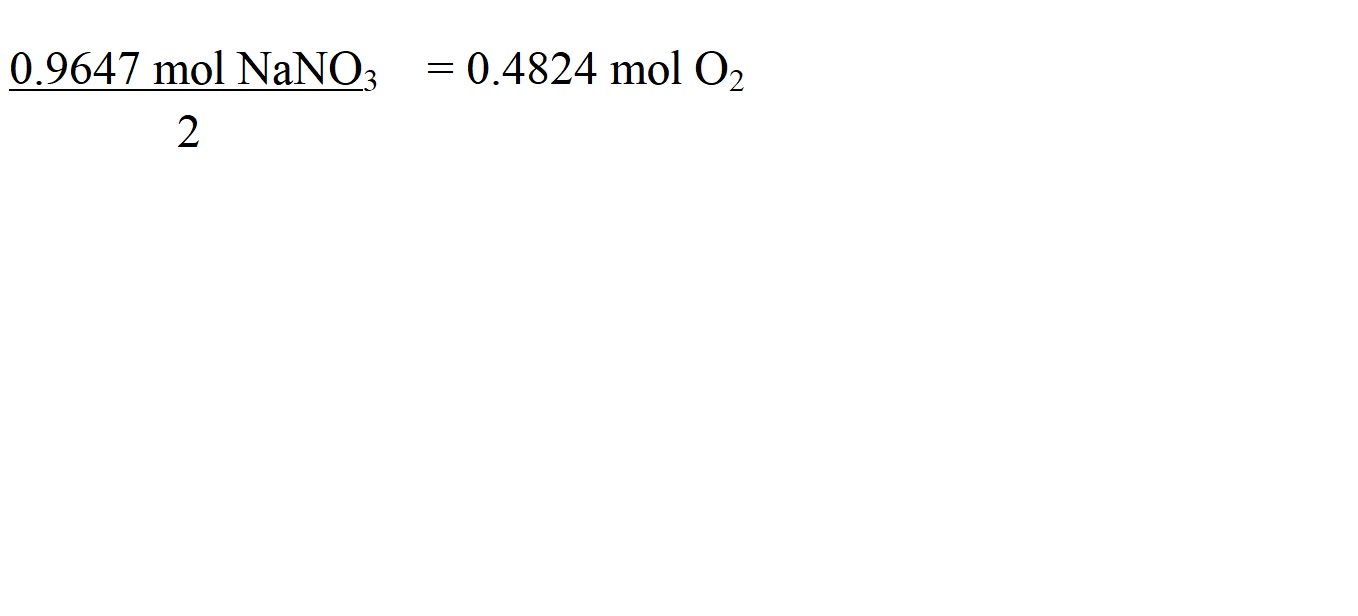
Step 6: Work out the molar mass of the substance you want to know the mass of – which is oxygen in this question.
M = 2 x 16.0 = 32.0 g mol-1
Step 7: Work out the mass of the substance using the molar mass and the amount in moles using the following formula:

This will then lead to the mass of oxygen and the final answer to the question. We are going to round our answer to three significant figures because the mass of the other substance we are given in the question is given in three significant figures.
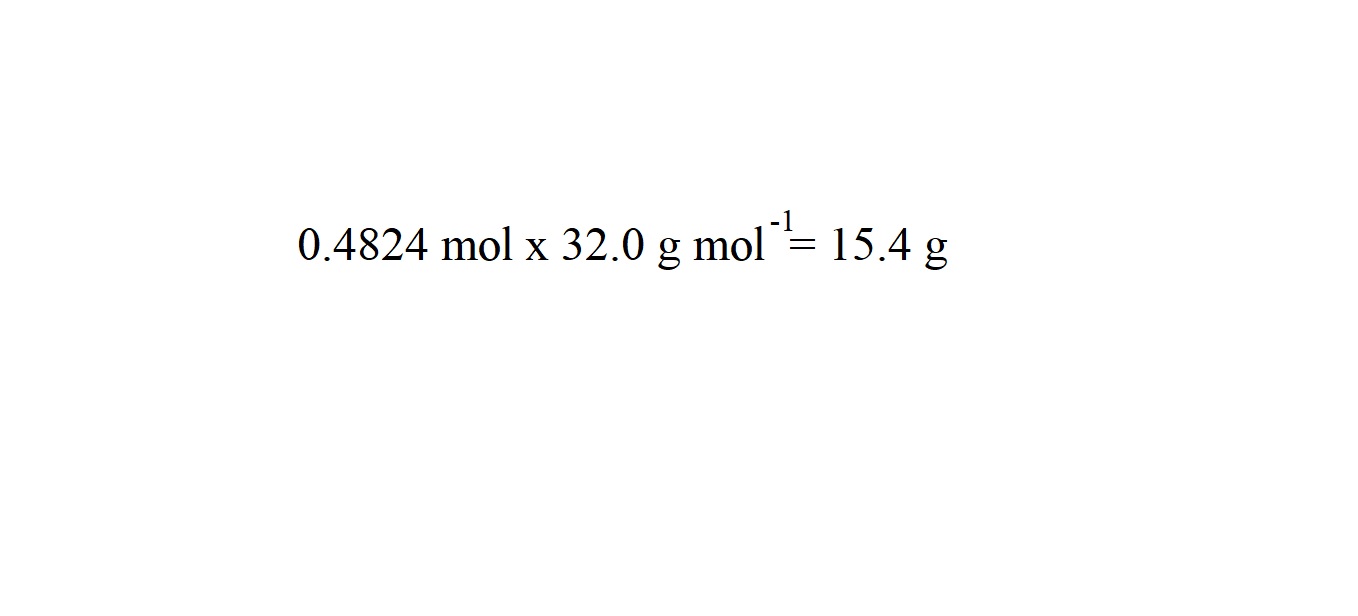
So we have worked out that 15.4 grams of oxygen are produced following the decomposition of 82.0 grams of sodium nitrate.
The aforementioned steps have been summarised in a table format below.
|
| 2NaNO3 | O2 |
| Mass (g) | 82.0 | 15.4 |
| Molar Mass (g mol-1) | 85.0 | 32.0 |
| Amount in Moles (mol) | 0.9647 | 0.4824 |
Amount in moles is divided by 2. Don’t forget about mole ratio.
Let’s try another question, only this time we are trying to work out the mass of a reactant in a forward reaction rather than a product. Steps 1 -4 and 6-7 involve the same processes – however step 5 – which involves mole ratio – is slightly different.
Question 2
Magnesium reacts with hydrochloric acid to produce magnesium chloride and hydrogen gas.
Calculate the mass of hydrochloric acid (HCl) needed to produce 27.5 g of magnesium chloride.
Step 1: Write out the equation.
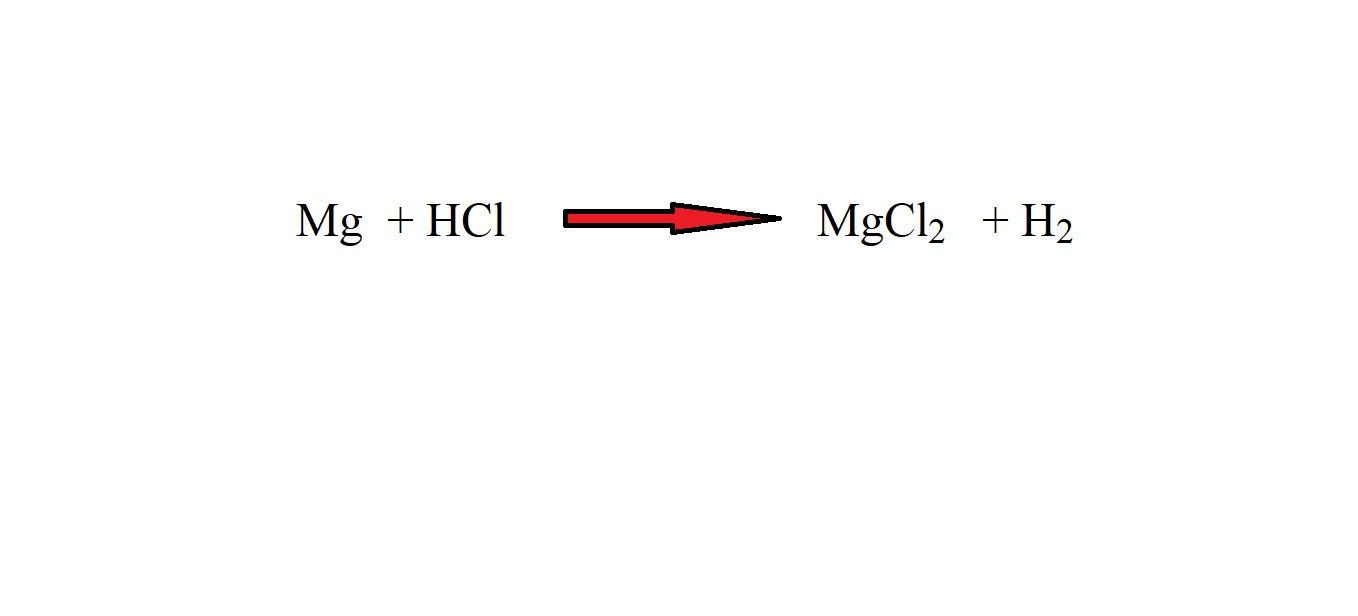
Step 2: Balance the equation with stoichiometric coefficients.
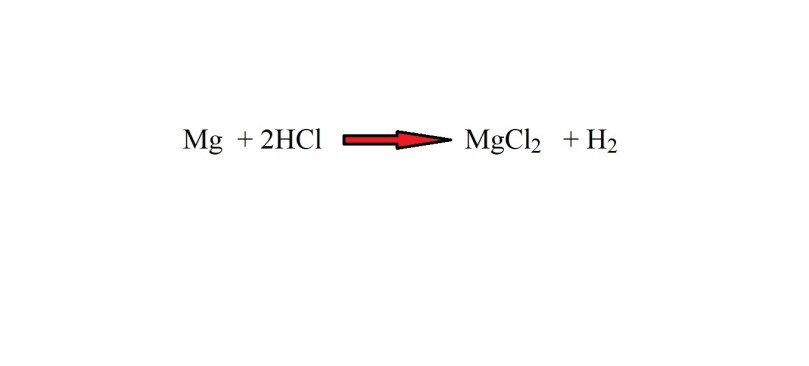
Step 3: Work out the molar mass of magnesium chloride.
M = 24.3 + (2 x 35.5) = 95.3 g mol-1
Step 4: Work out the amount in moles of magnesium chloride using the following formula.
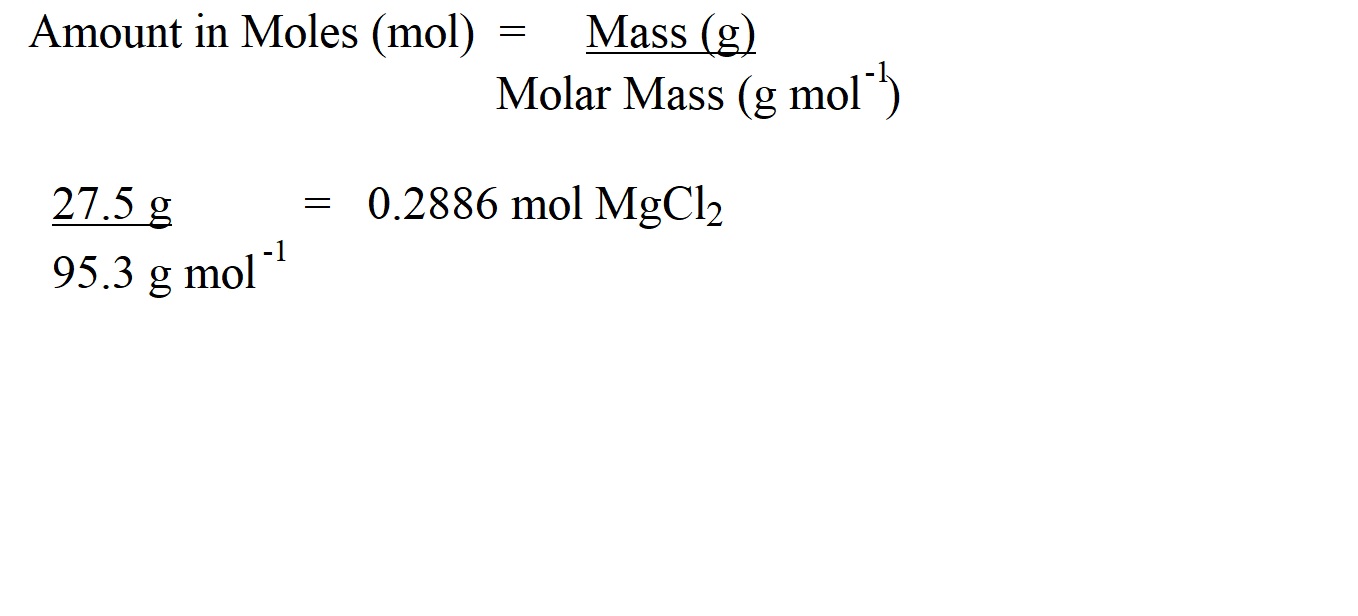
Step 5: Work out the amount in moles of hydrochloric acid using mole ratio. Let’s look at the balanced equation.
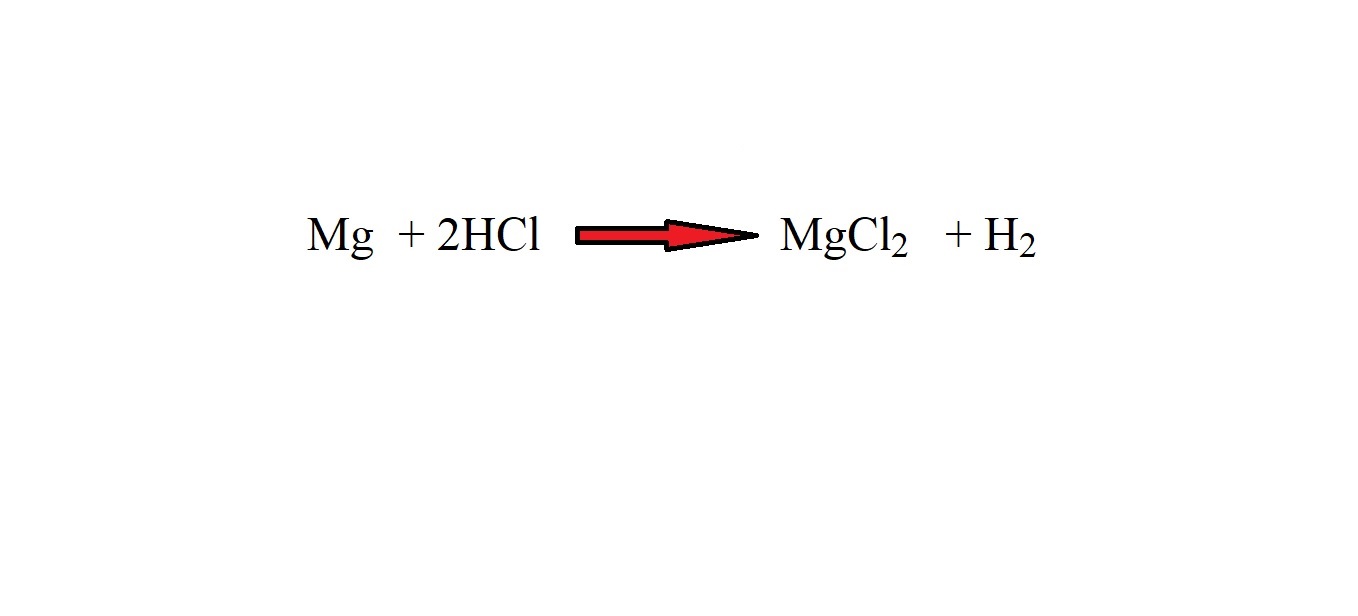
The mole ratio of hydrochloric acid to magnesium chloride is 2 moles to 1 mole. Therefore in order to work out how many moles of hydrochloric acid were involved as a reactant, we must multiply the amount in moles of magnesium chloride by 2.
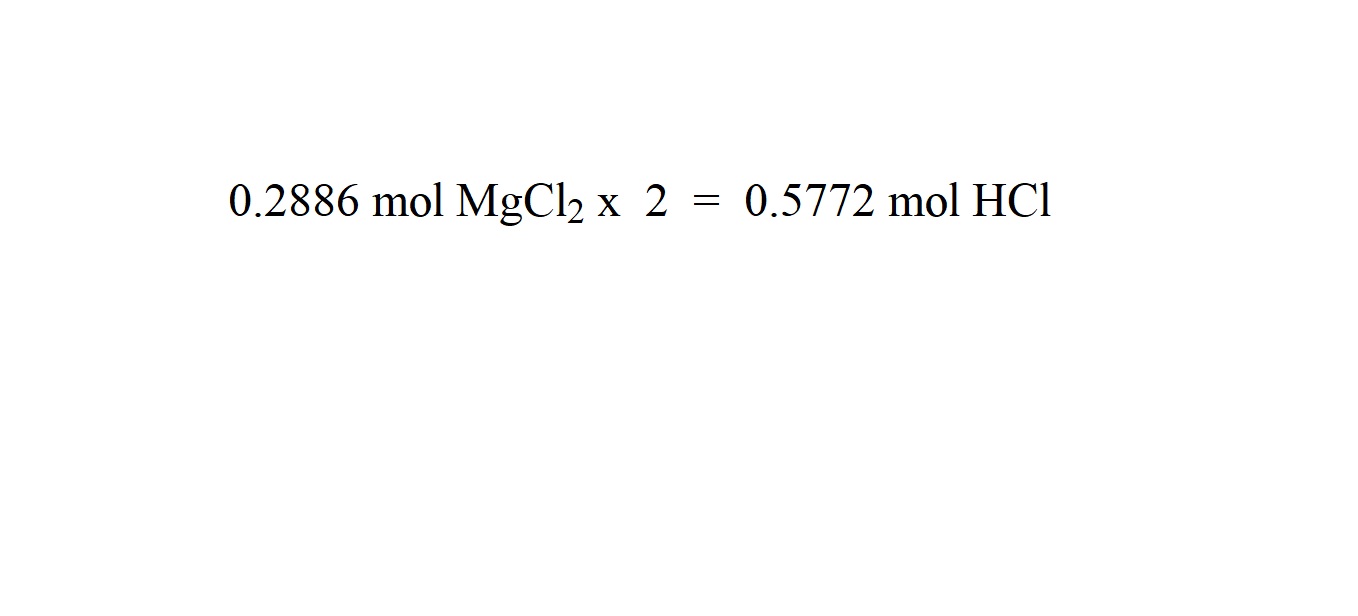
Step 6: Work out the molar mass of hydrochloric acid.
M = 1.01 + 35.5 = 36.51 g mol-1
Step 7: Work out the mass of hydrochloric acid using the following formula:

We are going to round the mass of hydrochloric acid to three significant figures because the mass of magnesium chloride is given in three significant figures.
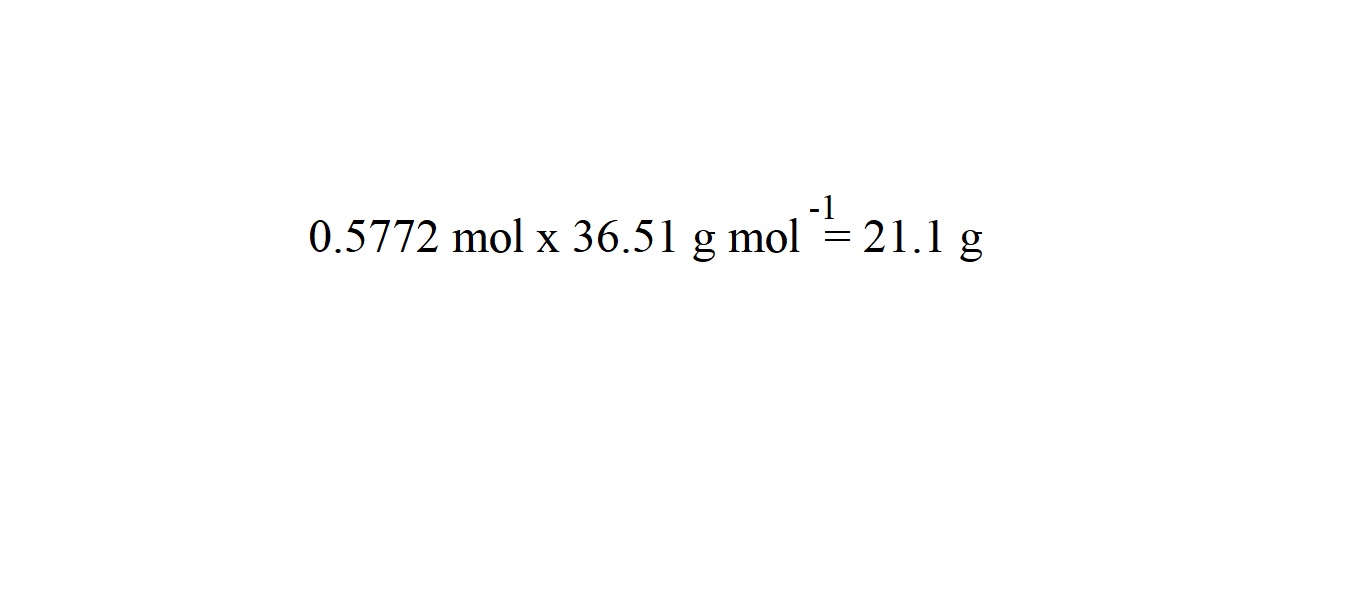
So we have worked out that 21.1 grams of hydrochloric acid is needed to react with magnesium to produce 27.5 grams of magnesium chloride.
The aforementioned steps have been summarised in a table format below.
|
| 2HCl | MgCl2 |
| Mass (g) | 21.1 | 27.5 |
| Molar Mass (g mol-1) | 36.51 | 95.3 |
| Amount in Moles (mol) | 0.5772 | 0.2886 |
Amount in moles is multiplied by 2. Don’t forget about mole ratio.
So there we go we have worked out the masses of chemical substances involved in a chemical reaction using a balanced chemical equation.
Over the next few tutorials on stoichiometry, we’ll be going through how to work out the number of particles involved either as a reactant or a product in a chemical reaction. We’ll also go over some more mole ratio problems.
Bye for now.
All images featured are my own.