Science and Joe

The following tutorial will cover how to calculate the masses of chemical substances involved in a chemical reaction via stoichiometric calculations using conversion factors to cancel out units.

If you would like to see how these calculations can be done without the use of conversion factors to cancel out units, please refer to ‘Determining the Masses of Reactants and Products of a Chemical Reaction (without Conversion Factors)’. Also, if you would like to see how chemical equations are balanced using stoichiometric coefficients and an explanation of some of the key terms and phrases of stoichiometry (e.g. stoichiometry coefficients and mole ratio) please also refer to ‘Determining the Masses of Reactants and Products of a Chemical Reaction (without Conversion Factors)’.

Reminder: A conversion factor is a fraction that consists of two equivalent values with different units of measurement. The main purpose of a conversion factor is to cancel out the unit we are converting from and only leave the unit we are converting to for an answer. In stoichiometry, that would initially be from grams to moles for the substance we know the mass of, but then from moles to grams for the substance we are working out the mass of.

This method first involves using the mass and molar mass of the substance we know the mass of to work out its amount in moles. We then use mole ratio to work out the amount in moles of the substance we want to know the mass of and then use its amount in moles and its molar mass to work out its mass.

Question 1

Gaseous ammonia reacts with copper (II) oxide (when heated) to produce copper, nitrogen gas and water.

If 14.50 grams of copper was produced, what was the mass of ammonia gas?

Step 1: Write out the reaction as an equation with the correct chemical formulas.

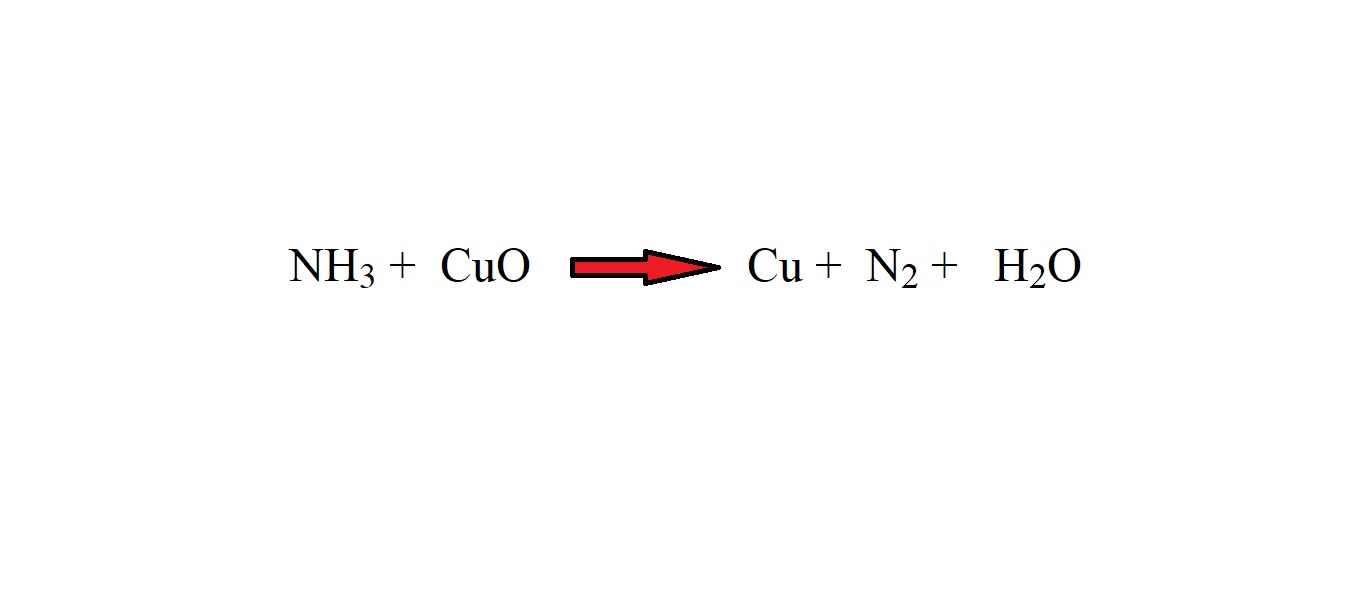
Step 2: Balance the equation with stoichiometric coefficients.

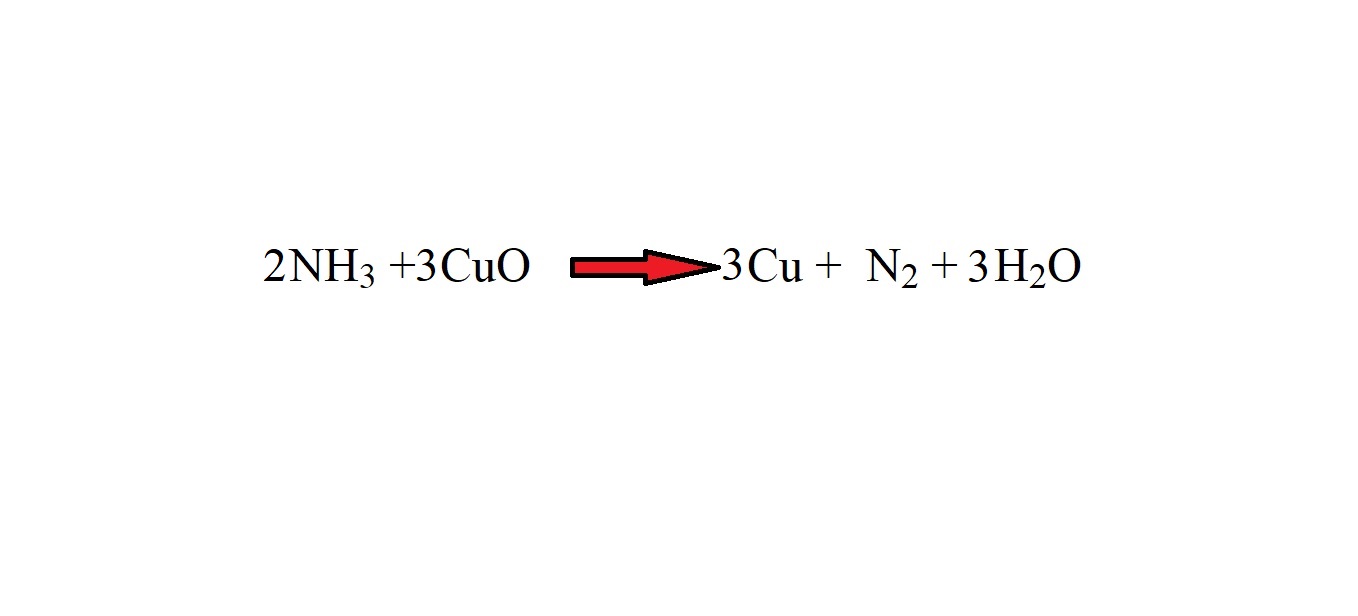
Step 3 :Work out the molar mass of the substance you know the mass of – which is copper.

M = 63.5 g mol^-1 (It’s just the relative atomic mass of copper.)

Step 4: Work out the molar mass of the substance you want to know the mass of – which is ammonia.

M = 14.0 + (3 x 1.01) = 17.03 g mol^-1

Step 5: Identify the mole ratio of ammonia to copper using the balanced equation.

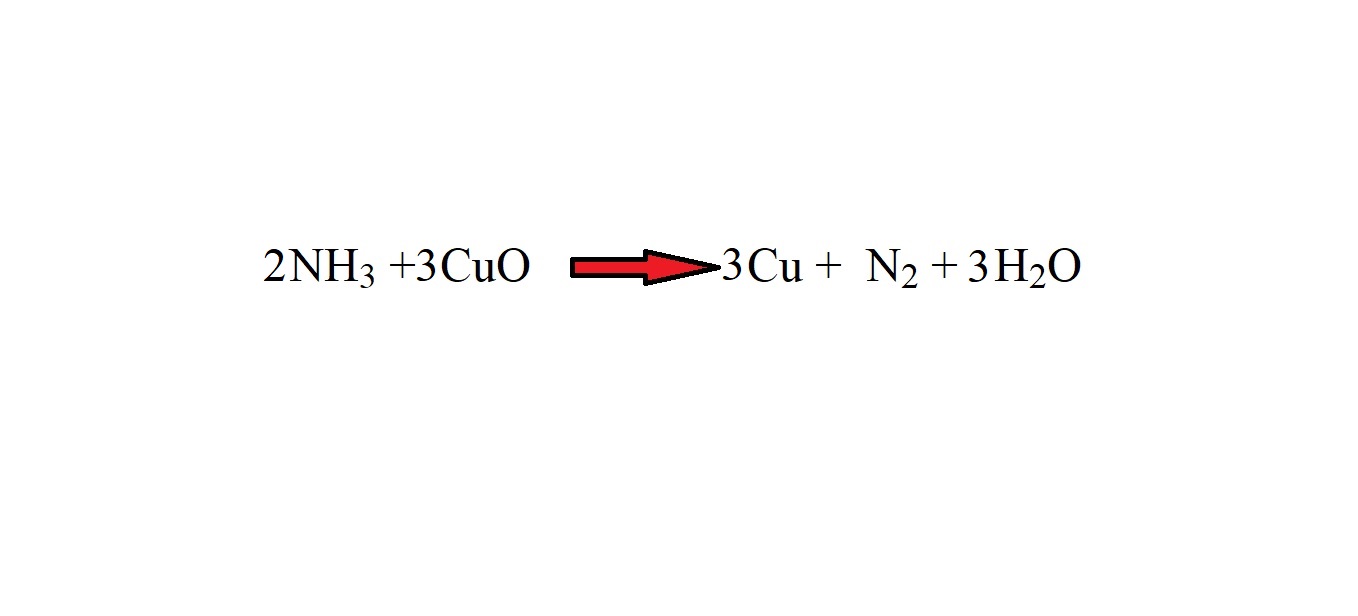
The balanced equation indicates that the mole ratio of ammonia to copper is 2 moles to 3 moles.

Step 6: Arrange the calculated molar masses and the mole ratio into conversion factors in a calculation and cancel units.

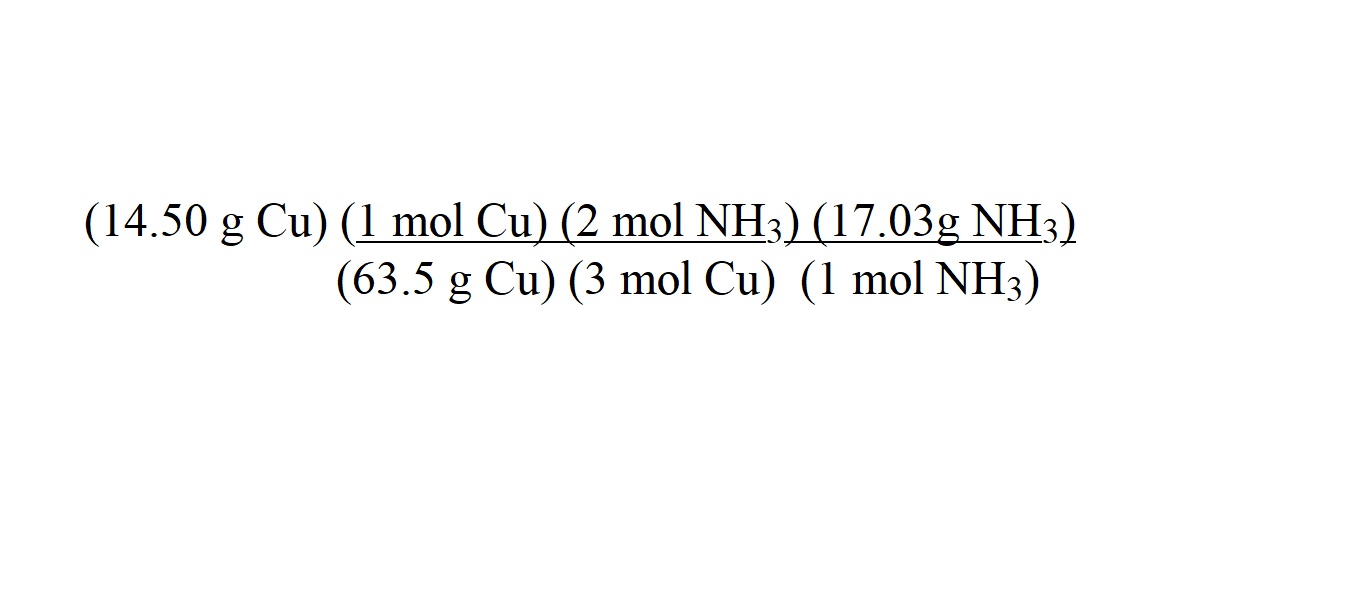
Note: Instead of including mol^-1 in the unit for molar mass, we replace it with the chemical formula of the substance when we include the value in a conversion factor.

The arrangement of three conversion factors in the above calculation allows us to cancel out the units we don’t want for our answer.

The first variable in the numerator is the mass of copper which is the substance we know the mass of. This is followed by a conversion factor consisting of the molar mass of copper and the equivalent value of 1 mole of copper. The second conversion factor indicates the mole ratio of ammonia to copper which is 2 moles to 3 moles. The third conversion factor consists of the molar mass of ammonia and the equivalent value of 1 mole of ammonia.

The arrangement of these values allows us to cancel out units by having the same units aligned to one another (diagonally) in the numerator and the denominator.

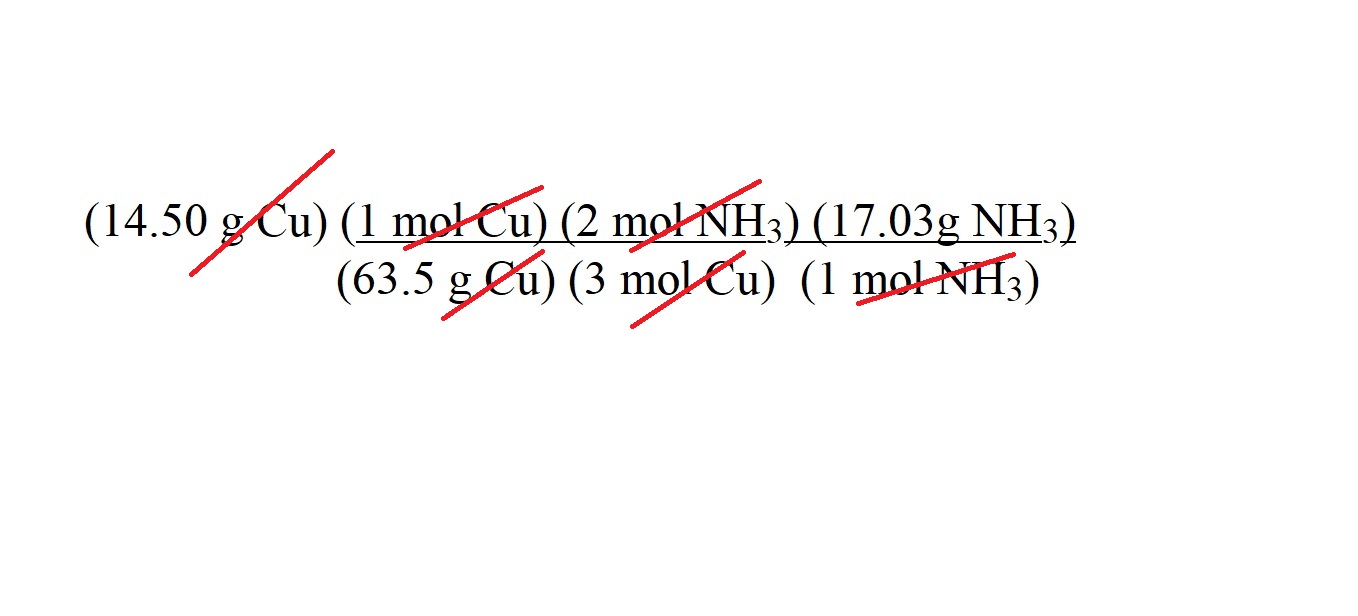
The units of g Cu cancel; the units of mol Cu cancel and the units of mol NH₃ cancel.

This then leaves only with the unit of g NH₃ which is the unit we want to use to express the mass of ammonia gas acting as a reactant.

Step 7: Carry out the calculation with only the unit we want for the answer.

We are going to round our answer to four significant figures because the mass of the other substance we are given in the question is given in four significant figures.

So we have worked out that 2.592 grams of ammonia gas acted as a reactant to produce 14.50 grams of copper.

Question 2

(This is an example of a reversible reaction.)

Nitrogen gas reacts with hydrogen gas to produce ammonia gas.

What mass of hydrogen gas is needed to produce 94.0 grams of ammonia gas?

Step 1: Write out the equation.

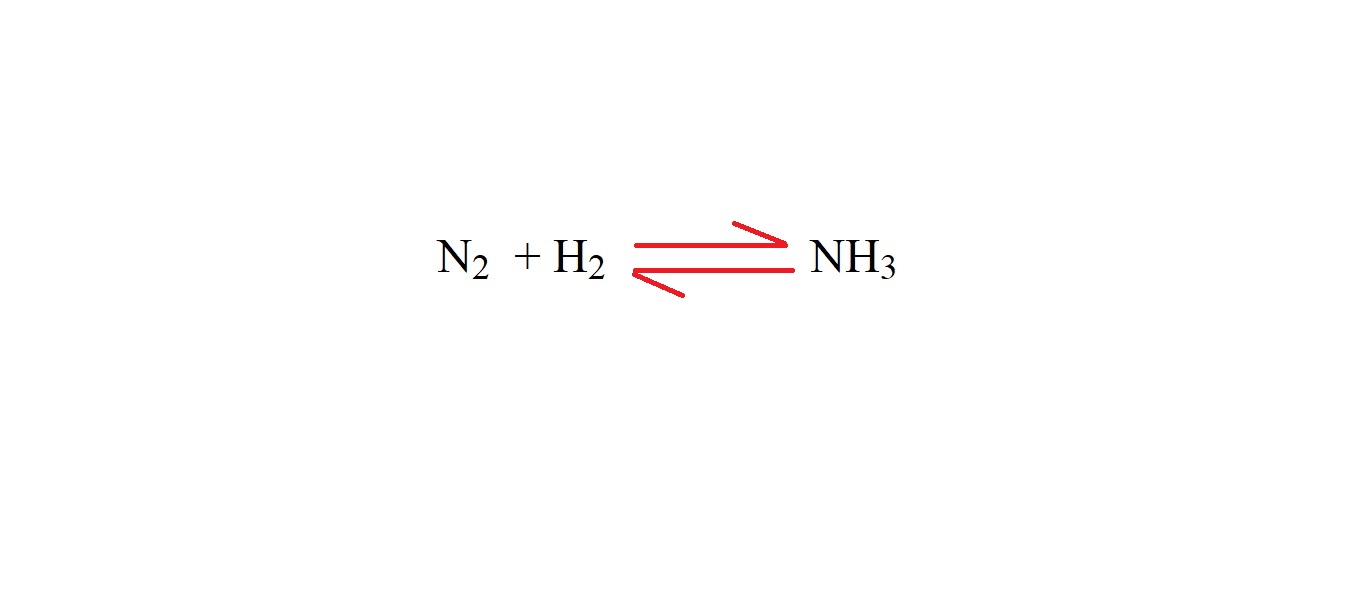
Step 2: Balance the equation with stoichiometric coefficients.

Step 3: Work out the molar mass of the substance you know the mass of – which is ammonia.

M = 14.0 + (3x 1.01) = 17.03 g mol^-1

Step 4: Work out the molar mass of the substance you want to know the mass of – which is hydrogen.

(Hydrogen exists as a diatomic molecule – meaning there is 2 atoms rather than 1.)

M = 2 x 1.01 = 2.02

Step 5: Identify the mole ratio of hydrogen to ammonia using the balanced chemical equation.

The balanced equation indicates that the mole ratio of hydrogen to ammonia is 3 moles to 2 moles.

Step 6: Arrange the calculated molar masses and the mole ratio into conversion factors in a calculation and cancel out units.

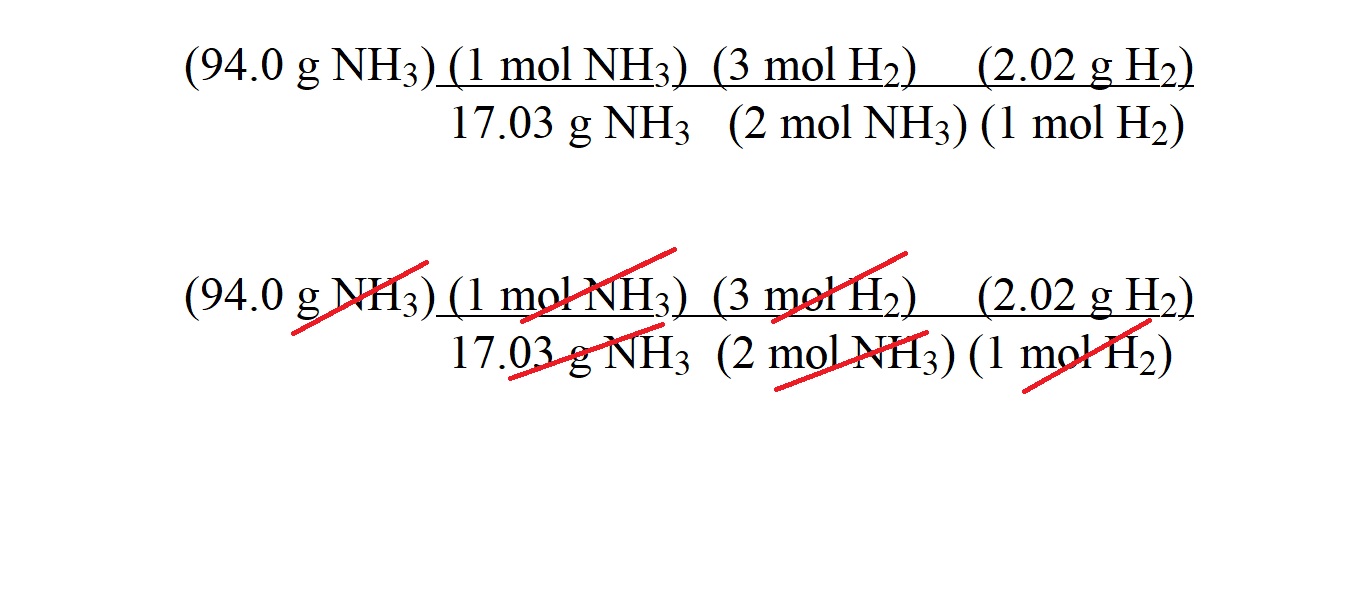
Step 7: Carry out the calculation with only the unit we want for the answer.

We are going to round our answer to four significant figures because the mass of the other substance we are given in the question is given in four significant figures.

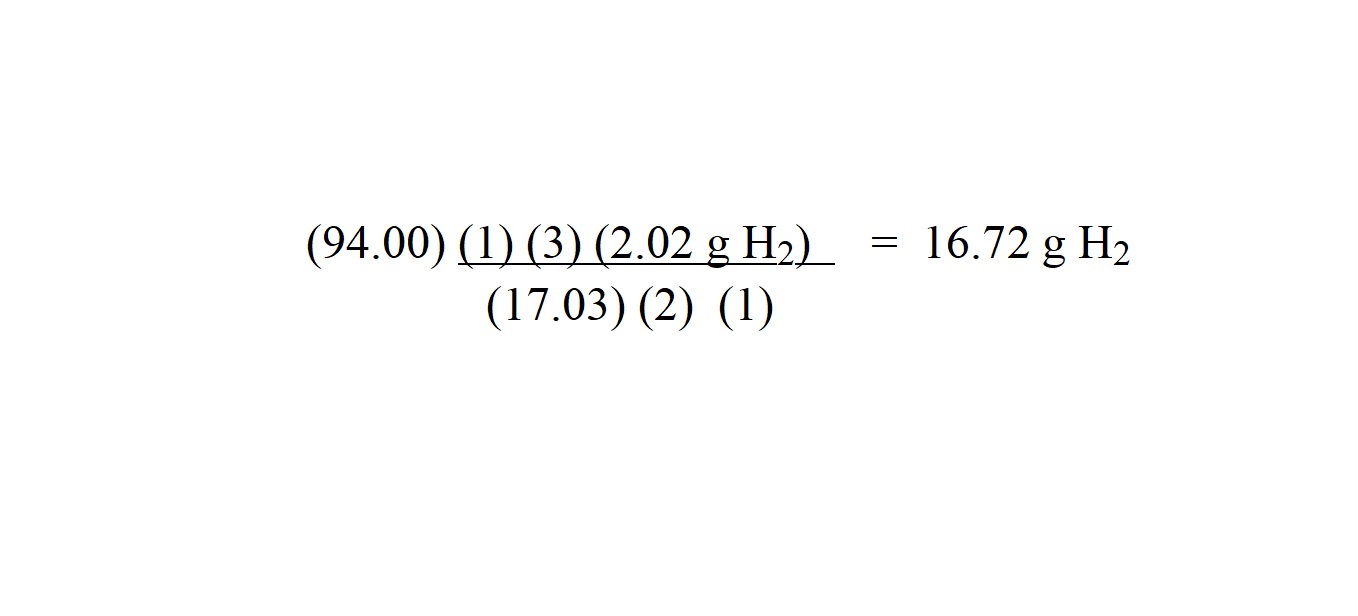
So we have worked out that 16.72 grams of hydrogen gas is involved as a reactant to produce 94.00 grams of ammonia gas.

So there we go we have worked out the masses of chemical substances involved in a chemical reaction using a balanced chemical equation and conversion factors to cancel out units. .

Over the next few tutorials on stoichiometry, we’ll be going through how to work out the number of particles involved either as a reactant or a product in a chemical reaction. We’ll also go over some more mole ratio problems.

Bye for now.

All images featured are my own.