
In this tutorial, we’ll go over some mole ratio questions while will involve calculating the amount in moles of a reactant or product using the amount in moles of a substance on the other side of a balanced chemical equation.
We are also going to be going over how to calculate the number of particles (atoms, molecules or formula units) that are acting as a reactant or is a product of a chemical reaction. This will be discussed in next tutorial – entitled ‘Determining the Number of Particles of a Reactant or a Product of a Chemical Reaction (with and without Conversion Factors)’.
Okay, let’s have a look at how we can use a mole ratio (also known as a stoichiometric ratio) to work out the amount in moles of a substance that is a reactant or a product.
If you wish to see how the MASS in grams of a reactant or a product of a chemical reaction is calculated, please see either ‘Determining the Masses of Reactants and Products of a Chemical Reaction (without Conversion Factors)’ or ‘Determining the Masses of Reactants and Products of a Chemical Reaction (with Conversion Factors)’.
Reminder: A mole ratio (also known as stoichiometric ratio) describes the ratio of the number of moles of one substance to the number of moles of another substance. This means for every certain number of moles of one substance that acts as a reactant in a forward reaction you will get a certain number of moles of another substance as a product.
Alternatively, it can indicate that a certain number of moles of a product reacts to form a certain number of moles of a reactant following a reverse reaction, because some reactions are reversible.
The mole ratio is determined by the stoichiometric coefficients that are in a balanced chemical equation. The stoichiometric coefficients are the numbers that are placed before chemical formulas, which allow a chemical equation to become balanced and for the law of conservation of mass to be fulfilled.
Please see ‘Determining the Masses of Reactants and Products of a Chemical Reaction (without Conversion Factors)‘ for a definition of the law of conservation of mass and further guidance on how to balance chemical equations.
The following questions will be answered using two methods: one involving the use of conversion factors and one without conversion factors.
Question
A reaction between magnesium and hydrochloric acid produces magnesium chloride and hydrogen gas.
How many moles of hydrochloric acid are needed to react with magnesium to produce 4.03 moles of magnesium chloride?
Step 1: Write out the reaction as an equation with the correct chemical formulas and balance the equation with stoichiometric coefficients.

Step 2: Determine the mole ratio between the substance you know the amount of in moles and the substance you want to know the amount of in moles.
According to the above balanced equation, if 2 moles of hydrochloric acid act as a reactant then 1 mole of magnesium chloride is produced.
Therefore, the mole ratio of hydrochloric acid to magnesium chloride is 2 moles to 1 mole.
The next step will depend on whether you use conversion factors. I’ll go through how to use both methods, but please check with your teacher, tutor or lecturer whether you should use conversion factors for your particular course.
Step 3 (without conversion factors): Multiply the amount in moles of magnesium chloride by 2 to work out the number of moles of hydrochloric acid needed as a reactant.
This is to account for the fact that 2 moles of hydrochloric acid are needed to produce 1 mole of magnesium chloride, therefore the amount in moles of hydrochloric acid acting as a reactant will be double the amount in moles of magnesium chloride produced.
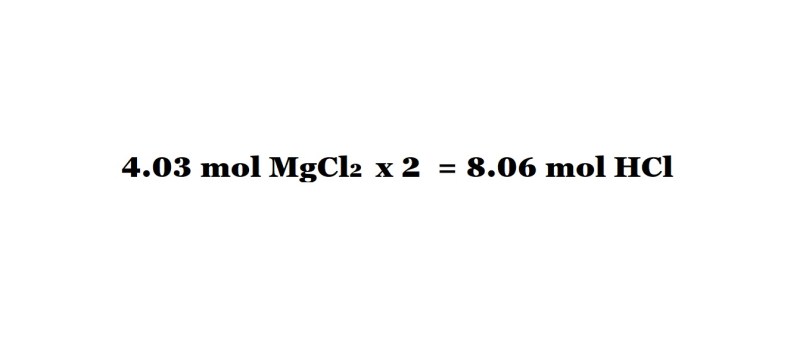
So once we multiply the amount in moles of magnesium chloride by 2, we find that 8.06 moles of hydrochloric acid are needed to produce 4.03 moles of magnesium chloride.
Let’s see how to do this with a conversion factor to cancel out the unit we don’t want for our answer – which is moles of magnesium chloride.
Step 3 (with conversion factors): Multiply the amount in moles of magnesium chloride by a conversion factor.
The conversion factor is determined by the mole ratio (stoichiometric ratio) between hydrochloric acid and magnesium chloride. The number of moles of hydrochloric acid according to the mole ratio is the numerator of the conversion factor and the number of moles of magnesium chloride according to the mole ratio is the denominator of the conversion factor.
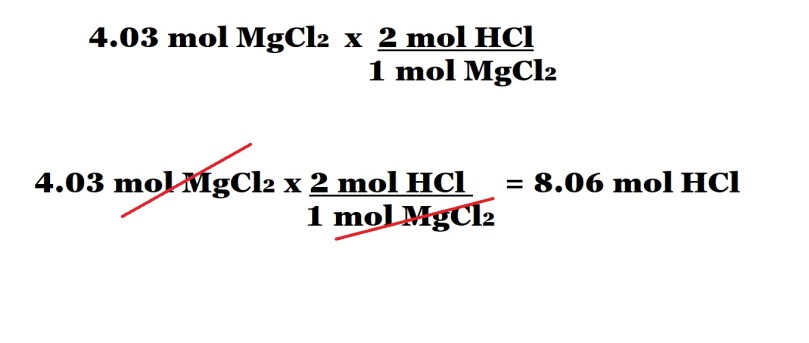
The placement of the number of moles of magnesium chloride according to the mole ratio as the denominator in the conversion factor allows us to cancel out the unit of moles of magnesium chloride because its at the top and the bottom. This just leaves us with the unit of moles of hydrochloric acid which is the unit we want for our answer.
We then multiply the original amount in moles of magnesium chloride (without the unit) by the number of moles of hydrochloric acid determined by the mole ratio and divide by the number of moles of magnesium chloride determined by the mole ratio. This gives us our final answer which is the amount in moles of hydrochloric acid acting as a reactant.
Okay let’s try another question, only this time we are asked to work out the amount in moles of two substances that are involved in a reaction.
Question
A reaction between aluminium and sulphuric acid produces aluminium sulphate and hydrogen gas.
How many moles of aluminium are needed to produce 2.11 moles of aluminium sulphate? How many moles of sulphuric acid are needed?
Similar to the previous question, we are given the amount in moles of one substance involved in the reaction – which is aluminium sulphate. However, this time we are asked to use this given information to work out the amount in moles of two other substances involved – aluminium and sulphuric acid.
Our first step – just like in the last question – is to write out the chemical equation that illustrates the reaction and balance it with stoichiometric coefficients.
Step 1: Write out and balance the reaction’s chemical equation.

We are now going to answer the rest of this question in two parts: the first will involve working out the amount in moles of aluminium involved as a reactant and the second part will involve working out the amount in moles of sulphuric acid acting as a reactant.
I will also once again go through the method that involves conversion factors and a method that doesn’t involve conversion factors. This will affect step 3.
Step 2 (Aluminium): Determine the mole ratio (stoichiometric ratio) of aluminium to aluminium sulphate.
According to the balanced chemical equation, the mole ratio of aluminium to aluminium sulphate is 2 moles to 1 mole.
Step 3 (Aluminium without conversion factors): Multiply the amount in moles of aluminium sulphate by 2 to work out the number of moles of aluminium that act as a reactant.
This is due to the mole ratio of aluminium to aluminium sulphate being 2 moles to 1 mole, which means the number of moles of aluminium acting as a reactant is twice the amount in moles of aluminium sulphate being produced.
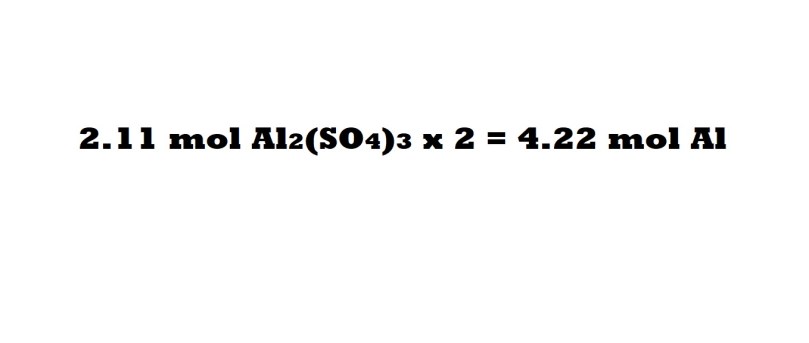
So according to this method 4.22 moles of aluminium act as a reactant to produce 2.11 moles of aluminium sulphate. Let’s now use the conversion factor method and see if we have the same answer.
Step 3 (Aluminium with conversion factors): Multiply the amount in moles of aluminium sulphate by a conversion factor. The conversion factor is determined by the mole ratio between aluminium and aluminium sulphate.
The number of moles of aluminium in the mole ratio is the numerator of the conversion factor and the number of moles of aluminium sulphate in the mole ratio is the denominator of the conversion factor.
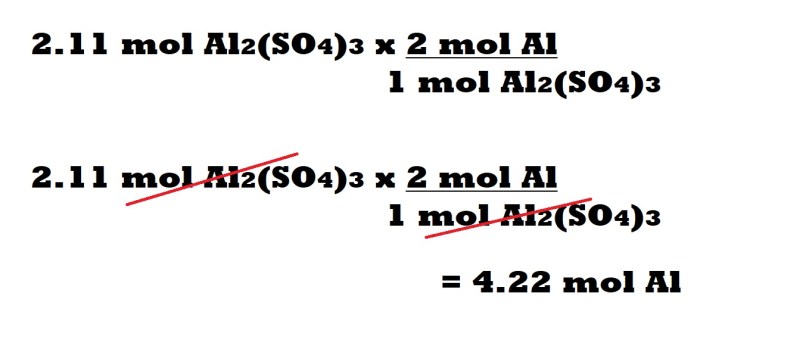
The cancellation of the unit of moles of aluminium sulphate allows us to only have the unit we want for our answer which is moles of aluminium.
We can then multiply the amount in moles of aluminium sulphate (without the unit) by the number of moles of aluminium within the mole ratio and divide it by the number of moles of aluminium sulphate within the mole ratio. This then leads us to our final answer which is that 4.22 moles of aluminium are needed as a reactant to produce 2.11 moles of aluminium sulphate.
Okay, so now we know the amount of aluminium we need, we can now work out the amount of sulphuric acid we need.
Step 4 (Sulphuric acid): Determine the mole ratio between sulphuric acid and aluminium sulphate.
According to the balanced chemical equation, the mole ratio of sulphuric acid to aluminium sulphate is 3 moles to 1 mole.
Step 5 (Sulphuric acid without conversion factors): Multiply the amount in moles of aluminium sulphate by 3 in order to work out the number of moles of sulphuric acid needed as a reactant.
This is due to the mole ratio of sulphuric acid to aluminium sulphate being 3 moles to 1 mole, which means the number of moles of sulphuric acid acting as a reactant is three times the amount in moles of aluminium sulphate produced.
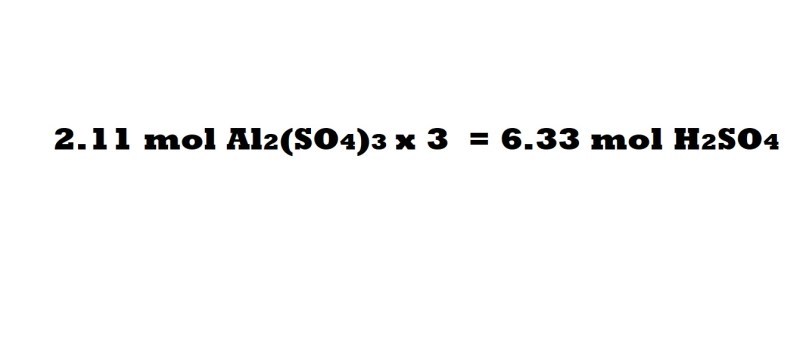
So according to this method 6.33 moles of sulphuric acid are needed as a reactant to produce 2.11 moles of aluminium sulphate. Let’s now use the conversion factor method to see if we get the same answer.
Step 5 (Sulphuric acid with conversion factors): Multiply the amount in moles of aluminium sulphate by a conversion factor. The conversion factor is determined by the mole ratio between sulphuric acid and aluminium sulphate.
The number of moles of sulphuric acid in the mole ratio is the numerator in the conversion factor and the number of moles of aluminium sulphate in the mole ratio is the denominator in the conversion factor.
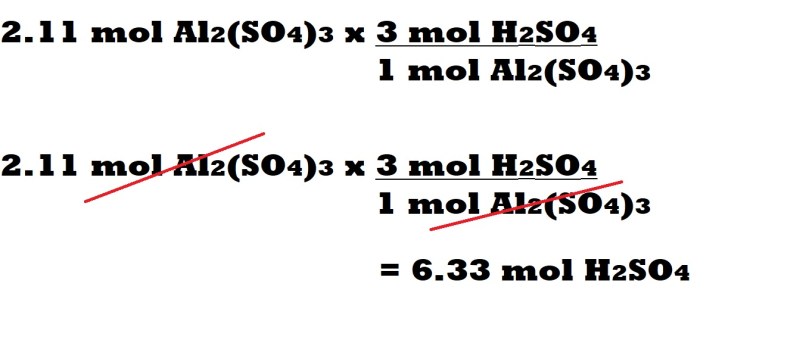
We can cancel out the unit of moles of aluminium sulphate which only leaves the unit of moles of sulphuric acid to include in our final answer.
We can then multiply the amount in moles of aluminium sulphate (without the unit) by the number of moles of sulphuric acid within the mole ratio and divide it by the number of moles of aluminium sulphate within the mole ratio. This then leads us to our final answer which is that 6.33 moles of sulphuric acid are needed as a reactant to produce 2.11 moles of aluminium sulphate.
So there we go, we have worked out the amounts in moles of various substances participating in a chemical reaction using mole ratio.
In the next tutorial, we will go through how to work out how many particles (atoms, molecules or formula units) are acting as a reactant or a product of a chemical reaction – using Avogadro’s number.
All images featured are my own.