
In the previous tutorial, we examined how to calculate the mass, amount and volume of a gas at standard temperature and pressure (STP). In this tutorial, we are going to calculate the same variables for gases in isolation and as part of a reaction – but at room temperature and pressure (RTP).
What is RTP?
Room temperature and pressure (RTP) denotes a temperature of 25oC (298.15 K) or 20oC (293.15 K) and a pressure of 1 atmosphere (101.325 kPa).
In these conditions, we can assume that 1 mole of a gas has a volume of 24 dm3 or 24 L. This will allow us to calculate the volume, mass and amount of a gas at RTP.
IMPORTANT NOTE:
There are differing opinions about the actual temperature of room temperature. Some educational resources will state that the temperature for RTP is 20oC (293.15 K) and some will state it’s 25oC (298.15 K).
Please note that the volume of 1 mole at RTP would still be 24 dm3 or 24 L and it will usually be stated in a question that you are working at RTP.
Calculating at RTP
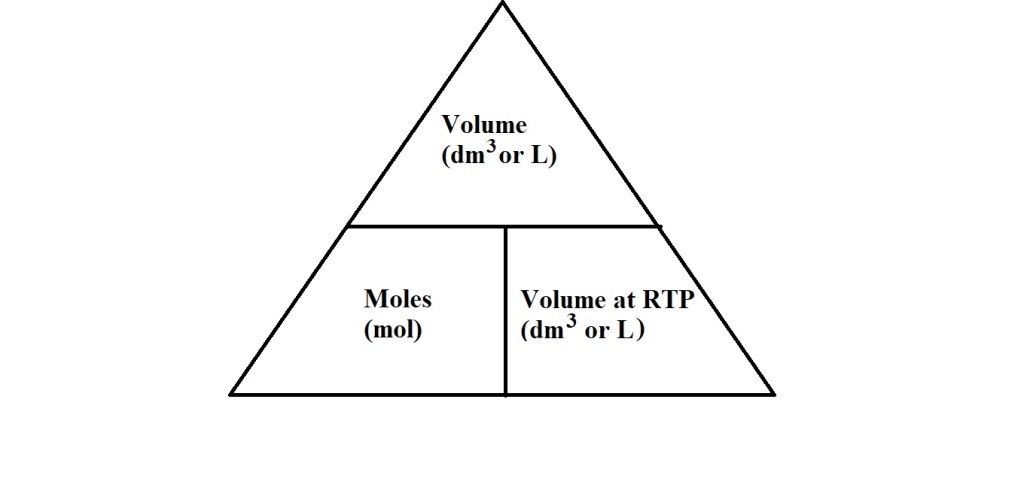
The triangle above may be a familiar sight as this is often used to summarise mole and volume calculations at RTP in textbooks or other resources. Let’s take a look at the equations that this triangle summarises.
Equations for Calculating Volume at RTP

Equations for Calculating Amount in Moles at RTP

What about mass?
The calculation of the volume and the amount of a gas at RTP has already been summarised – but what if you are asked to calculate the mass of a sample of a gas?
If you are given the volume of a gas you will first need to calculate the amount of the gas in moles at RTP. This can be done with the following equation:

Once you have worked out the amount in moles, you will have to calculate the mass of the sample of the gaseous substance in grams. This can be done with the following equation:

Let’s look at some questions and breakdown our working step-by-step.
Calculating Volume at RTP
Question: What is the volume in litres of 3.48 moles of O2 at RTP?
Working:
We’ll need the following equation:

Reminder: Always be wary of the units you are asked to express. In this question we are asked to express volume in litres.
You can complete this question with a conversion factor to cancel out the unit we don’t want for our answer and include the unit we want for our answer.
Reminder: A conversion factor is a fraction that consists of two equivalent values with different units that allows for the cancellation of a unit we don’t want for our answer and the conversion to a unit we want for our answer.
The unit we want to convert to is in the numerator in the conversion factor and the unit we to want to convert from and therefore cancel out is the denominator in the conversion factor. Unit conversion takes place upon the multiplication of a value by a conversion factor.
IMPORTANT NOTE: The conversion factor method is required for some specifications but not others. Please check with your teacher, tutor or lecturer whether your course requires the conversion factor method. I will demonstrate how these calculations can be carried out with a conversion factor and without a conversion factor in this tutorial.
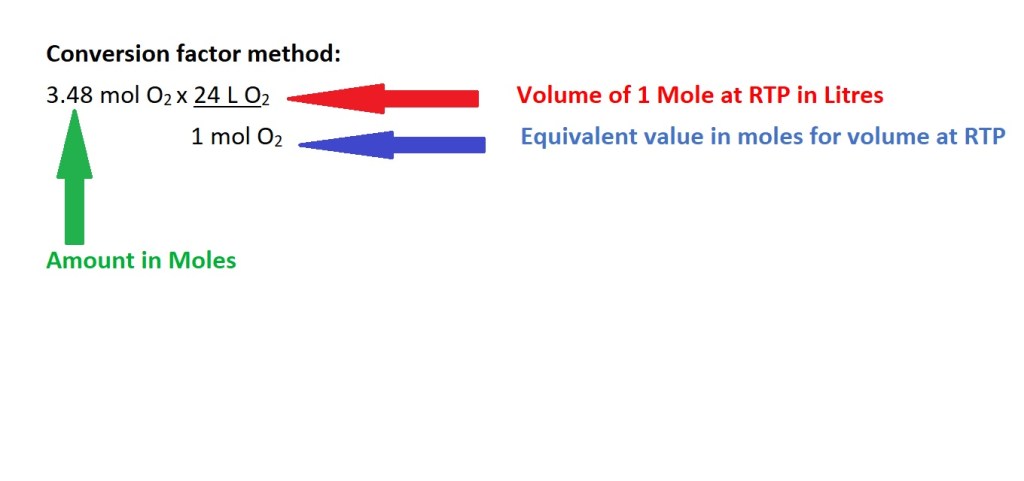
The conversion factor above consists of the volume of 1 mole of a gas at RTP as the numerator as it has to correspond with the previous equation which states we must multiply this value by the amount in moles to calculate the volume.
The denominator is the equivalent value of 1 mole as the volume of 24 L is the volume of 1 mole of a gas at RTP. The sole purpose of this value is to allow for the cancellation of the unit of mol to convert to the unit we need for volume which is litres (L).
We can now cancel out the unit we don’t want for our answer and leave the unit we want for our answer.


Note: We are going to include the same number of significant figures in our answer as there are in the value in the question with the fewest significant figures. The value in the question with the fewest significant figures has three significant figures and therefore our final answer will be given to three significant figures.
Answer: 83.5 L O2
Question: What is the volume in dm3 of 63.0g of chlorine gas (Cl2 ) at RTP?
Working:
We need to carry out two steps:
- Convert the mass of chlorine gas into amount in moles.
We can do this by using the following equation:


Note: We need to calculate the molar mass of a diatomic molecule of chlorine because this is one of the elements that usually exists as a diatomic molecule when not bonded to other elements.
The conversion factor for this calculation is different to the one in the previous calculation because the equation dictates that the molar mass must be the denominator because we are dividing by it. The equivalent value is 1 mole of chlorine because the molar mass is the mass of 1 mole of the substance. However, the unit we want to cancel out is still in the denominator of the conversion factor and the unit we want for our answer is in the numerator.


Note: We write the molar mass with the unit of g mol-1 for the non-conversion factor method followed by the relevant chemical symbol.
Note: We have written the amount in moles in four significant figures because this is not the final answer to the question and we want to avoid rounding to too few significant figures prior to reaching our final answer to avoid inaccuracy.
2. Convert from amount in moles to volume in dm3.
You’ll need the following equation:


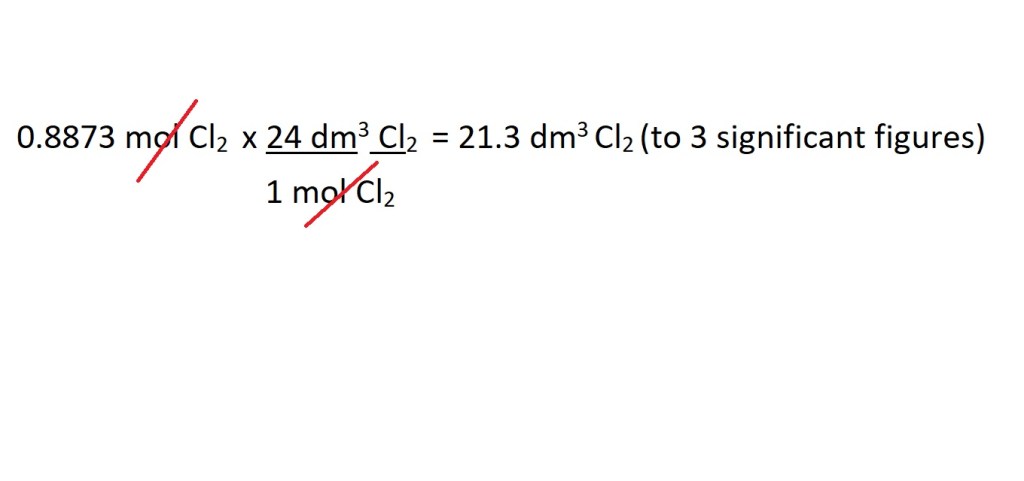

Answer: 21.3 dm3 Cl2
Question: What volume of ammonia (NH3) is produced from 43.0 dm3 of N2 reacting with H2 at RTP?
Working:
This requires multiple steps and it’s important to check your answer to each individual step.
- Write out a balanced chemical equation that represents the reaction (if one is not already provided).
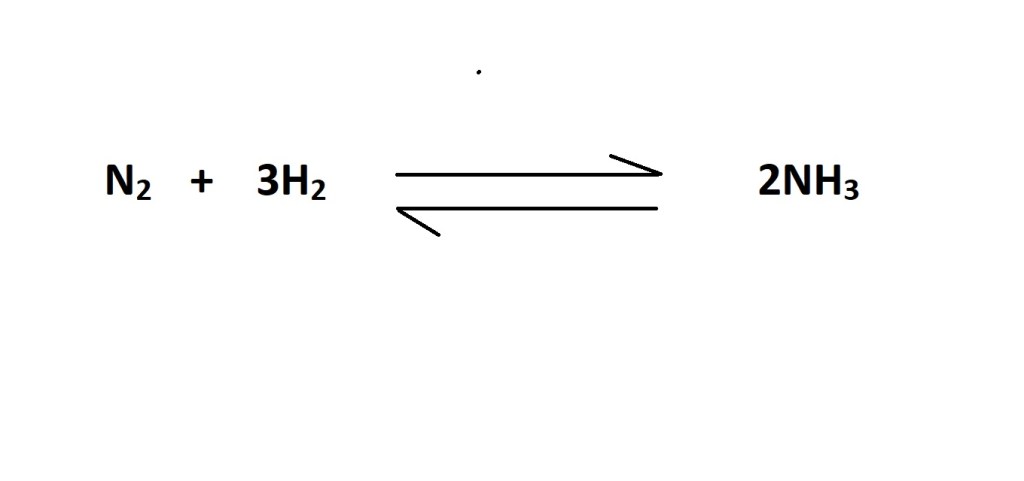
2. Convert the volume in dm3 of N2 into amount in moles.


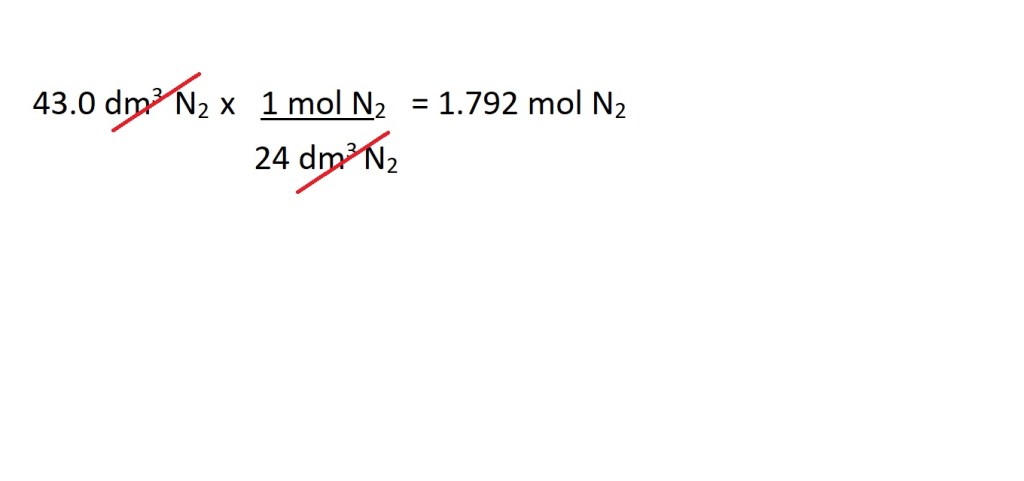

3. Convert from the amount in moles of nitrogen to the amount in moles of ammonia using the mole ratio (stoichiometric ratio) in the balanced chemical equation.
Reminder: The mole ratio (stoichiometric ratio) is the number of moles of a substance to the number of moles of another substance according to a balanced chemical equation. This could be the number of moles of a product produced from a certain number of moles of a reactant or the number of moles of one reactant that reacts with a certain number of moles of another reactant.

The balanced chemical equation states that 3 moles of nitrogen react to produce 2 moles of ammonia, therefore the mole ratio is 3 moles of hydrogen to 2 moles of ammonia.
We can now use this mole ratio to convert from moles of nitrogen to moles of ammonia as follows:
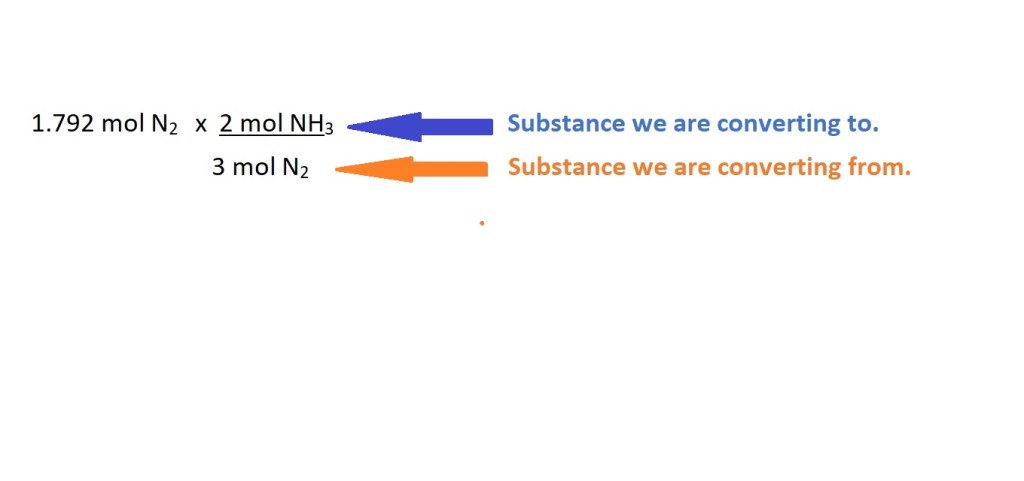
To allow us to cancel out the unit we don’t want we must ensure we put the mole ratio value of the substance we want to convert from as the denominator and the mole ratio value for the substance we want to convert to as the numerator.
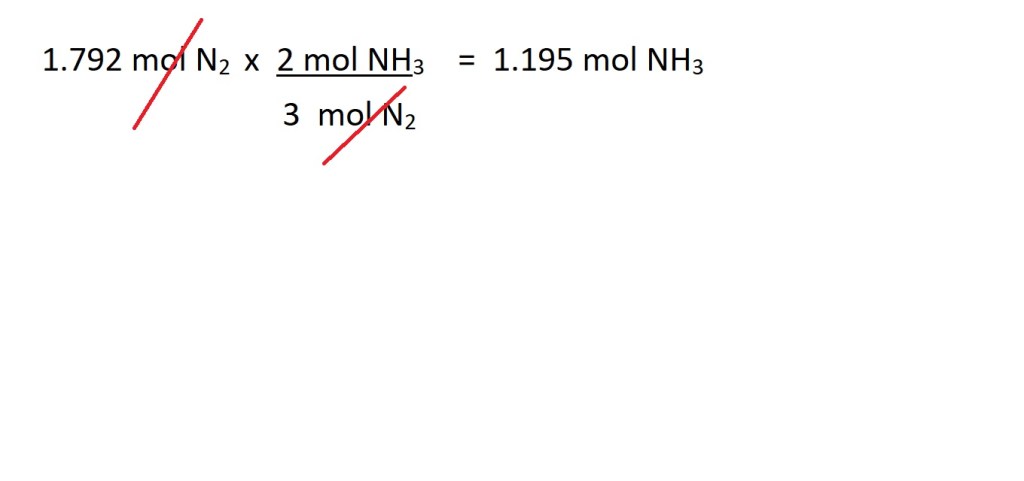
4. Calculate the volume of ammonia using the amount in moles.




Answer: 28.7 dm3 NH3
Calculating the Amount in Moles at RTP
Let’s now take a look at some questions in which we are asked to work out the amount in moles of a gas in a given volume at RTP.
Note: These questions will involve steps that we have used previously – however it’s important to know when to use certain steps and when not to use certain steps.
Question: How many moles are present in 85.0 L of helium gas (He) at RTP?
Working:


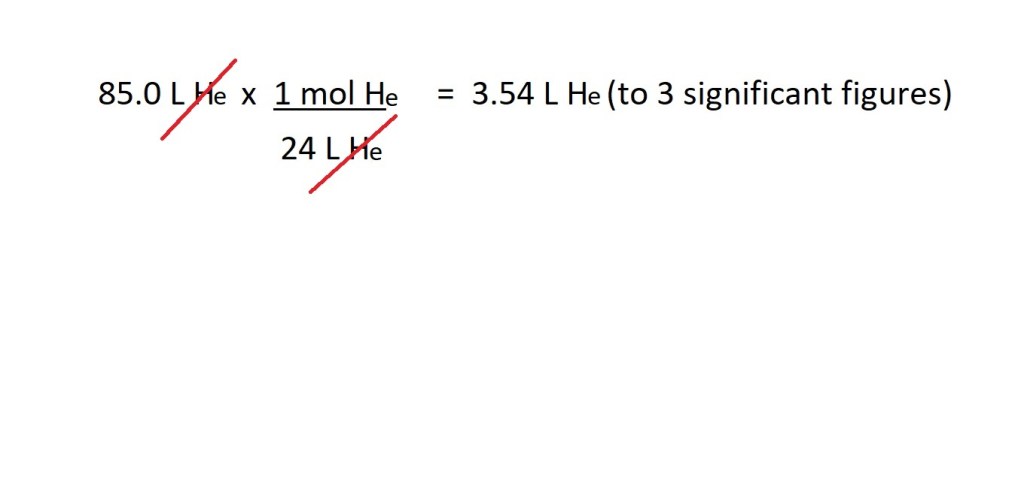

Answer: 3.54 L He
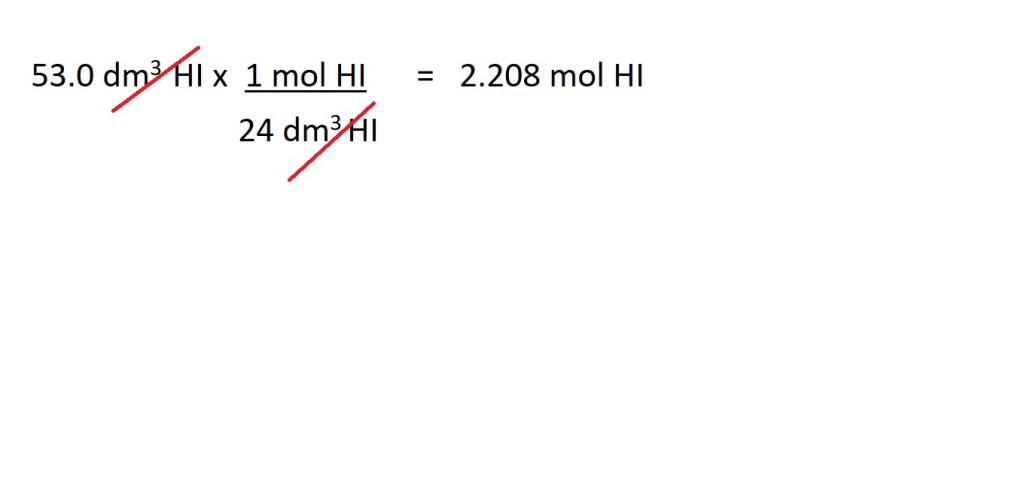
Question: How many moles of iodine gas (I2) react with hydrogen gas (H2) to produce 53.0 dm3 of hydrogen iodide gas (HI) at RTP?
Working:
A couple of steps are required and once again we should check each individual step as we go along.
- Write out the balanced chemical equation for the reaction if one isn’t provided.
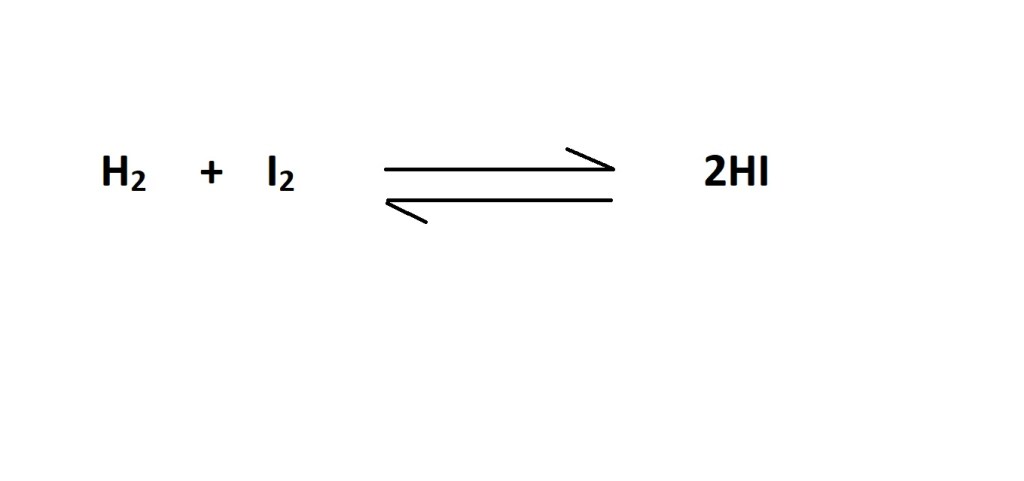
2. Convert the volume of hydrogen iodide in dm3 to amount in moles of hydrogen iodide.



3. Convert from moles of hydrogen iodide (HI) to moles of iodine gas (I2) using the mole ratio (stoichiometric ratio) determined by the balanced chemical equation.
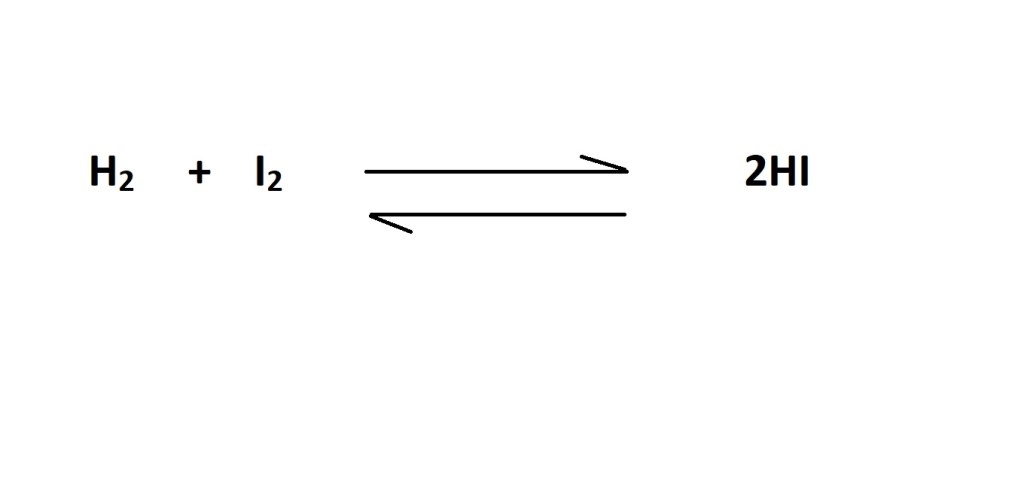
The balanced chemical equation states that 2 moles of hydrogen iodide (HI) are produced from 1 mole of iodine gas so the mole ratio is 1 mole of iodine gas to 2 moles of hydrogen iodide.
We can now use this mole ratio to convert from moles of hydrogen iodide to moles of iodine gas as follows:

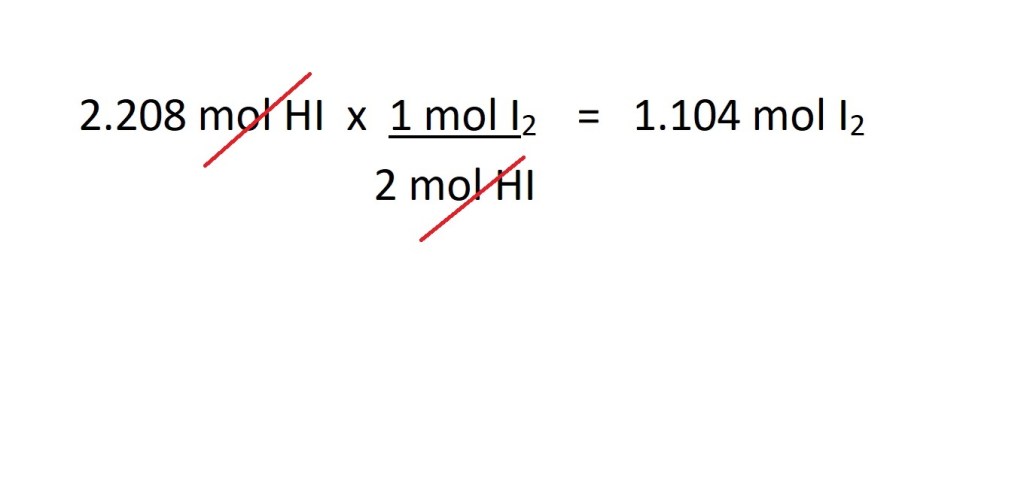
4. Convert from moles of iodine gas to volume of iodine gas in dm3.




Calculating Mass at RTP
Question: What is the mass in grams of 45.0 dm3 of argon gas (Ar) at RTP?
Working:
- Convert the volume of argon gas into amount in moles.


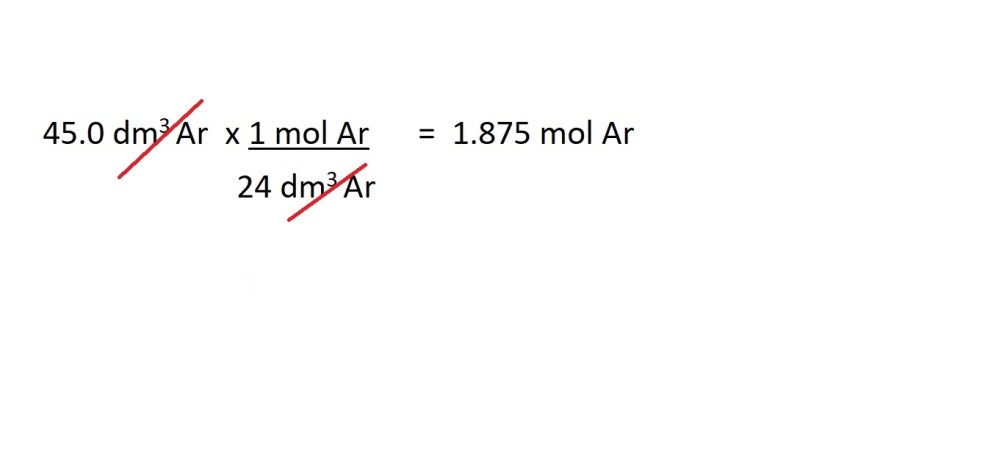

2. Convert the amount in moles of argon gas into mass in grams.


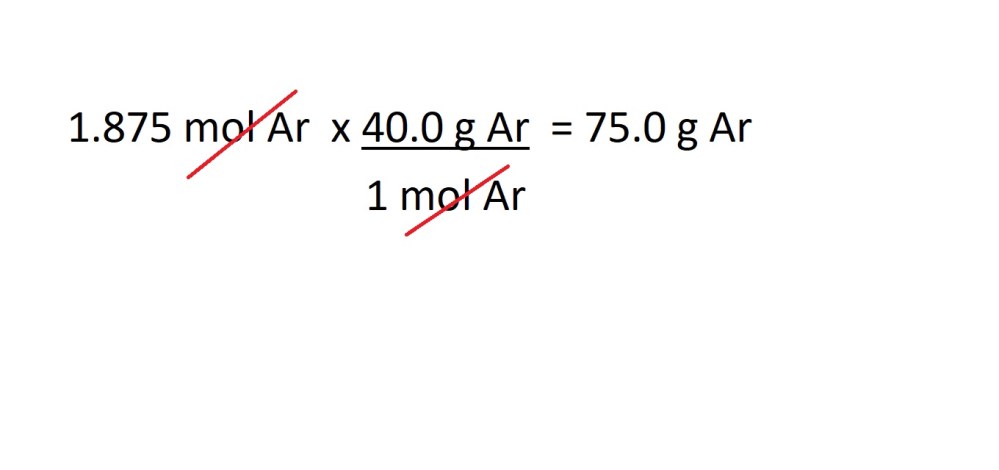

Answer: 75.0 g Ar
Question: What is the mass in grams of butane gas (C4H10) that reacts with oxygen (O2 ) upon combustion to produce 25.0 L of carbon dioxide (CO2) and water (H2O) at RTP?
Working:
This is another multiple step process, but let’s break it down step-by-step and don’t forget to check each individual step as you go along.
Note: This is the kind of question that you must read very carefully. You are given all 4 of the substances involved in the reaction – however only 2 should be involved in the calculation.
- Write out a balanced chemical equation that represents the reaction (if one isn’t already provided).
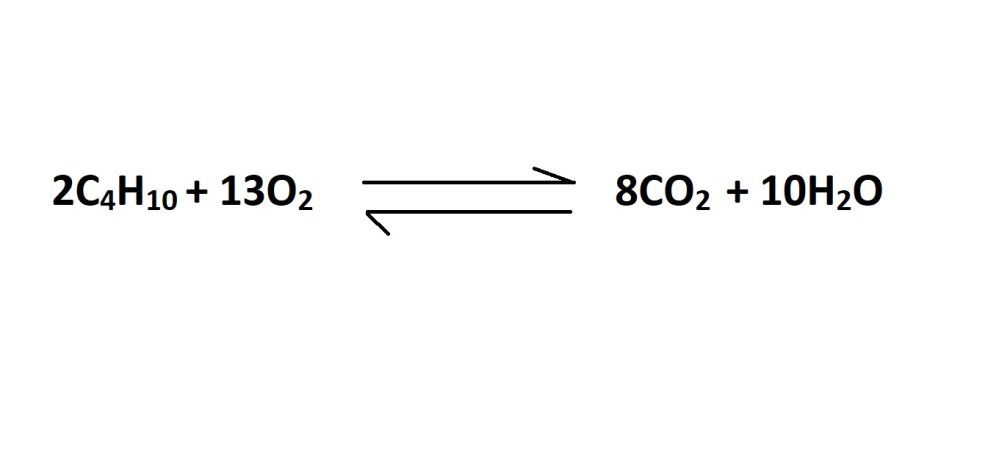
2. Convert the volume of carbon dioxide in litres into amount in moles.


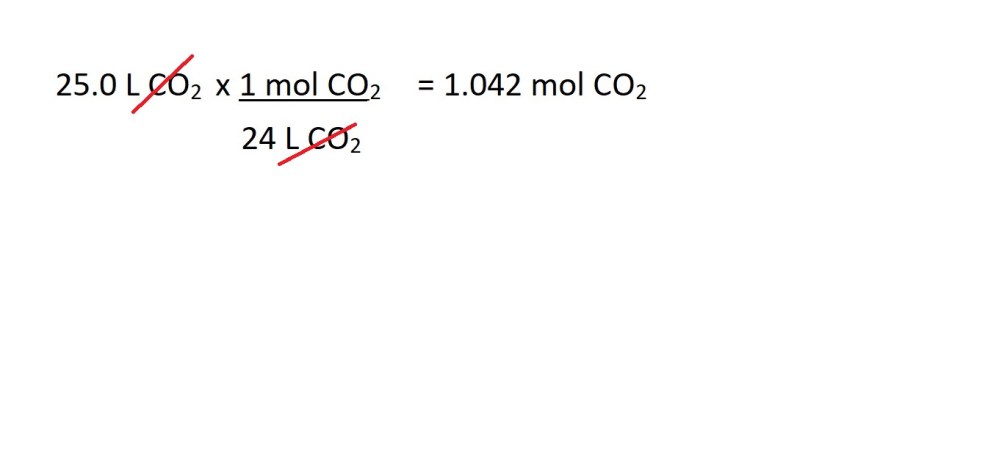

3. Convert from moles of carbon dioxide to moles of butane gas using the mole ratio (stochiometric ratio) according to the balanced chemical equation.
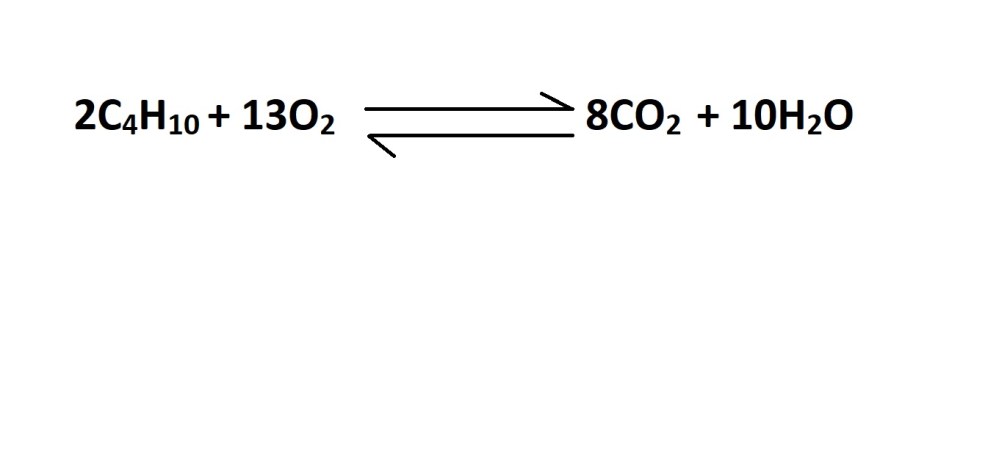
The balanced chemical equation states that 2 moles of butane gas reacts during the production of 8 moles of carbon dioxide. Therefore, the mole ratio is 2 moles of butane gas to 8 moles of carbon dioxide.
We can now use this mole ratio to convert from moles of carbon dioxide to moles of butane gas as follows:
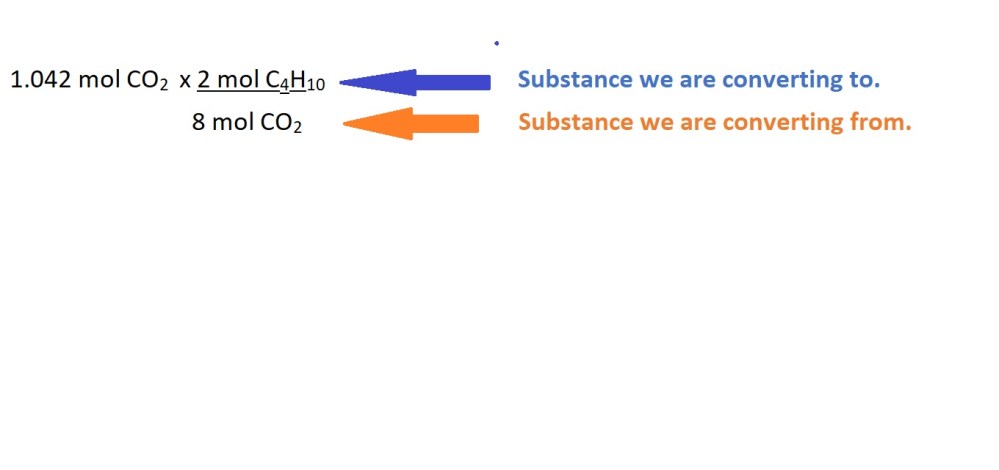
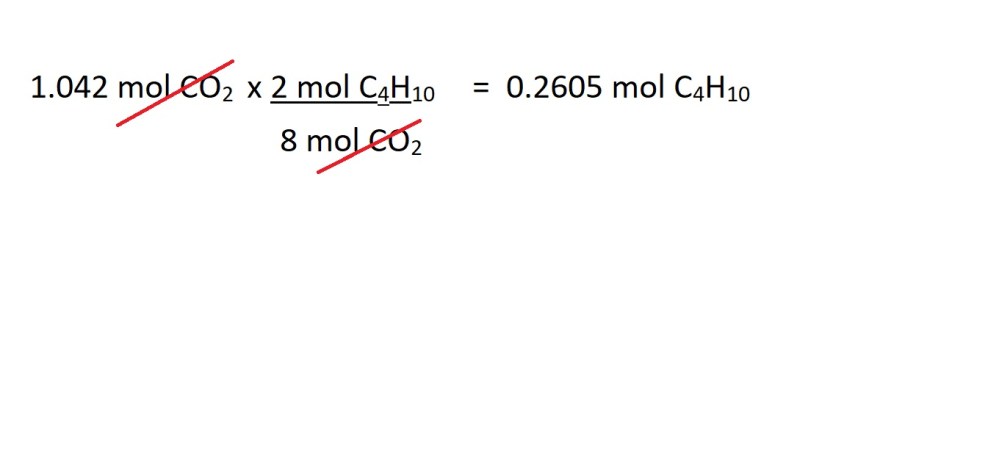
4. Calculate the mass of butane gas in grams using the amount in moles.

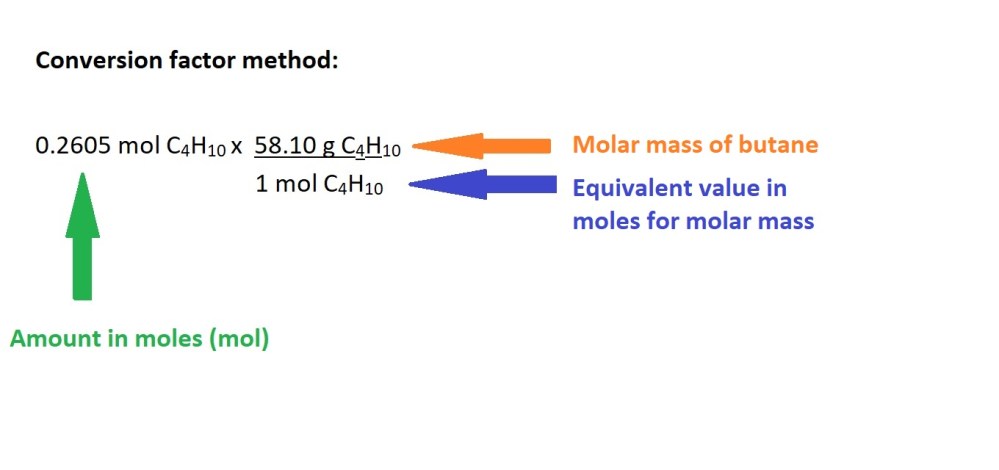


Answer 15.1 g C4H10
The past two tutorials have focused on calculations involving gases in very specific conditions – STP and RTP. However, what if the conditions in which a gas is situated differs to the strict conditions that are required for STP and RTP? If that is the case, we will require the ideal gas law.
In the next tutorial, we will explore the ideal gas law including how it was devised and how it can be used for calculations involving gases in most conditions.